Today, strange bedfellows. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

Students will tell you math and science fit together like hand and glove. But do they?

The question was vividly brought to my attention when reading the book Infinitesimals, by Amir Alexander. Today we see math and science as inseparable. But at their most basic, they're worlds apart. Math relies on deductive reasoning. We start with basic principles then logically deduce their consequences. In the world of math, if you believe what you start with - sets, numbers, addition, and so on - there's no uncertainty about your conclusions. None.

Science doesn't work that way. Scientists observe the world around them, then reach inductive conclusions. If every swan a scientist observes is white, he may reasonably theorize that all swans are white. However, if a black swan shows up at the party, his theory needs to be modified or discarded. Einstein's theory of general relativity showed how Newton's theory of gravity was wrong - or at least incomplete. Yet Newton rightly remains one of the most highly esteemed scientists in history.

In his book, Alexander makes a case that science didn't arise against a backdrop of ignorance, but against a backdrop of muddled math-like reasoning. If the great edifice of mathematics could be erected on a foundation of clear, unequivocal truths, why couldn't the same approach be employed to, say, explain motion, or erect the edifice of a perfect system of government? Alexander argues that Thomas Hobbes was inspired to his seventeenth century political views by the precision of Euclid's geometry. Hobbes foresaw the natural rise of a Leviathan - a commonwealth of citizenry freely accepting the absolute rule of a dictator. And, says Alexander, Hobbes argued his position with the precision of a mathematician. 

Photo Credit: Wikimedia

Of course, the precision of Hobbes argument is open to debate. But the point Alexander makes is a good one. Be it a theory of government or a scientific theory, math-like reasoning can't stand front and center. Devoid of grounding in observed facts, such reasoning is all sound and fury, signifying nothing. Descartes. The scholastics. The shores of history are riddled with the remains of those seduced by the precision of math. For all math's beauty, power, and even perfection, when it comes to science, math's but a humble servant - though admittedly a pretty good one. Our universe, it turns out, is surprisingly mathematical.

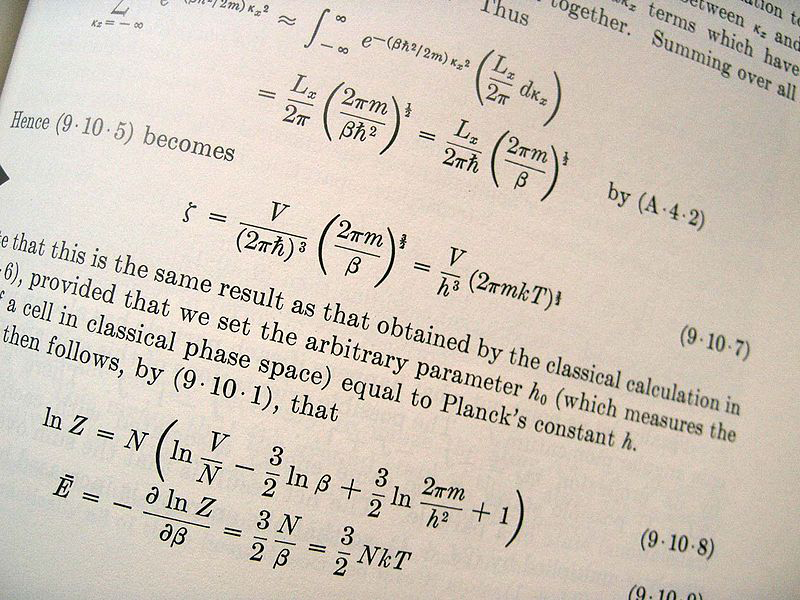
Photo Credit: Wikimedia

Which is why, even today, scientists are sometimes tempted by the siren call. They offer up infinite universes we can't interact with; bona-fide physical dimensions beyond three that can't be experimentally verified. "But the math," goes the argument, "is too compelling to ignore." Is it? Or are we once again falling into that age-old trap?

Photo Credit: Flickr

I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work. 

(Theme music)

For a related episode, see INDIVISIBLES.

Amir Alexander. Infinitesimal: How a Dangerous Mathematical Theory Shaped the Modern World. New York: Scientific American / Farrar, Straus and Giroux, 2014.

This episode was first aired on April 6, 2017