Indivisibles
by Andy Boyd
Today, indivisible. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
It's mystifying to see what small things people can argue about. But what may seem small to outsiders can be enormous to those involved.
Such was the case in seventeenth century Italy. Bonaventura Cavalieri was a contemporary and friend of Galileo. Galileo encouraged Cavalieri to work with a new mathematical technique for calculating the volume of objects. A 3-dimensional cube can be thought of as a stack of 2-dimensional squares laid atop one another like a stack of papers. Thus, we can get the volume of the cube by adding up the height of the individual papers. Cavalieri called the paper-like sheets indivisibles.

Bonaventura Cavalieri. Photo Credit: Wikimedia
The problem with indivisibles is that they were assumed to have a thickness of zero, and no matter how many times you lay sheets of zero thickness on one another, their combined thickness is still zero. Or is it? What if we laid an infinite number of sheets on top of one another? How would that add up?
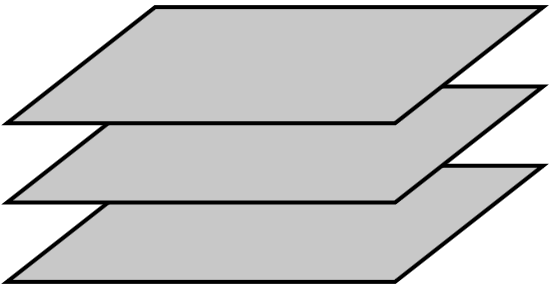
Photo Credit: Wikimedia
It was a problem philosophers had dealt with since at least the time of the ancient Greeks: when the infinitely big meets the infinitely small, things can get messy. The reason Cavalieri's technique was of interest at all was because it was useful. It allowed him and those that followed in his footsteps to calculate the volume of all sorts of interesting new shapes.
Cavalieri's Indivisibles. Photo Credit: Wikimedia
Still, the technique was so controversial it caused an uproar. For one reason, if it wasn't applied carefully it could lead to erroneous results. The Italian was edging toward discovery of integral calculus, but important details needed working out.
Another reason for controversy was that scholars at that time had difficulty separating mathematical abstraction from the real world. It wasn't enough to use Cavalieri's technique to calculate and leave it at that. Scholars argued over the issue of whether, say, bricks, for example, were really made of thin sheets of matter. If they weren't, then calculating the volume of a brick as if these sheets existed was heretical.
Yet another cause for controversy was that indivisibles were at odds with the heavenly geometry of Euclid and Aristotle, whose writings profoundly influenced Roman Catholic philosophy of the day. Church scholars were busy reasserting themselves in the wake of the Protestant Reformation, and anything that didn't fit established Church doctrine was frowned upon, as Galileo had discovered. The Revisors General, a committee of Jesuits tasked with making pronouncements on science, outlawed the teaching of indivisibles within the vast, influential network of Jesuit schools. As such, the study of indivisibles dwindled in Italy and elsewhere in the Roman Catholic sphere of influence.
It's not clear that Italian mathematicians would've made the step from indivisibles to calculus had their work continued. But we do know Cavalieri's pioneering work made its way to France and England, where calculus would appear some half-century later. Indivisibles were a small thing, but they could've been big.
Photo Credit: Wikimedia
I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
Amir Alexander. Infinitesimal: How a Dangerous Mathematical Theory Shaped the Modern World. New York: Scientific American / Farrar, Straus and Giroux, 2014.
This episode was first aired on March 9, 2017