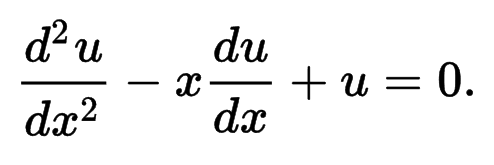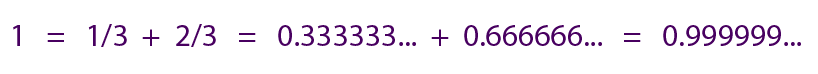Limits
by Andy Boyd
Today, taking it to the limit. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Perhaps the most central yet confounding theme in higher math is infinity. Once students hit calculus, which confronts the infinitesimally small, there's no turning back.
A Differential Equation. Photo Credit: Andy Boyd
One of the twentieth century's great mathematicians, David Hilbert, told a story about what's come to be known as Hilbert's Grand Hotel. Hilbert asked us to imagine a hotel with an infinite number of rooms labeled 1, 2, 3, and so on to infinity. One day a visiting dignitary came looking for a room, but learned they were all occupied. The dignitary turned to leave, but was called back by the proprietor. 'We may be full, but we still have room,' he said. He then sent a note to all the guests asking them to move to the room that was numbered one higher than the room they were in. This in turn freed up room 1 for the dignitary.

Sopot Grand Hotel. Photo Credit: Wikimedia
Not only could the proprietor handle one extra guest, he could've made room for an infinite number. How? By asking everyone in the hotel to move to the room with a number two times larger than their room number. This would've left all the odd rooms available for the new guests. When working with infinity, the concepts of fulland no space available are not one and the same.
As another example of how strange infinity can be, consider the number .9999... with the 9's running off to infinity. You might want to think of it as the number that's just a little, tiny-bit smaller than the number one. But you'd be wrong. It is the number one. If you don't believe me, add one-third and two-thirds on your calculator.
An equation proving the equality of 1 and .99999... Photo Credit: Andy Boyd
Such oddities are forced on us by the logical foundations that underlie math. And the examples just mentioned are merely the tip of the iceberg. The more deeply we peer into the realm of the infinite, the more we find results that seemingly make no sense. 'Logic,' lamented mathematician Henri Poincaré, 'sometimes makes monsters.'
Yet, even as we seek to tame infinity, we limit ourselves from taking the final step. Literally. The limit is the most essential tool in the arsenal for dealing with the infinite. Looking at the summation 1 + 1 + 1 ... continuing forever, mathematicians don't say the sum is infinite. They say that in the limit as we add more and more ones, the summation can be made bigger than any large but finite number. We're allowed to get ever closer to infinity, but we're not allowed to reach the edge and look over. Ah, but that the human mind was capable of taking it to the limit.
I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
0.9999... From the Wikipedia website: https://en.wikipedia.org/wiki/0.999. Accessed January 17, 2017.
Hilbert's Paradox of the Grand Hotel. From the Wikipedia website: https://en.wikipedia.org/wiki/Hilbert's_paradox_of_the_Grand_Hotel. Accessed January 17, 2017.
This episode was first aired on January 19, 2017