A Case for Three Dimensions
by Andy Boyd
Today, a case for three. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Why do we live in a world of only three physical dimensions? It's probably not something you've given a lot of thought to. But it's a hard question to avoid when working with math, where moving from three to four dimensions is as easy as adding a variable to an equation.
The question confronted me when I ran into a 1917 paper by physicist Paul Ehrenfest. Ehrenfest asked how gravity might work in a universe with more than three dimensions. As it turns out, not very well.
.png)
Paul Ehrenfest. Photo Credit: Wikimedia
To understand why, let's first consider something quite different: the amount of paint required to cover a large ball. Suppose it takes us a quart to get a nice, even coating. Now consider a ball with a radius that's twice as big. How much paint is needed to cover this larger ball?

Open Soy Paint Can. Photo Credit: Flickr
The surface area of the larger ball proves to be four times that of the smaller one. So we'd need four quarts of paint or, alternatively, we could stick with one quart, but the coating would have to be one-fourth as thick.
It turns out that the pull of gravity works in much the same way. Move to a distance twice as far from the sun, and the gravitational pull drops to one-fourth of what it was. Metaphorically, it's as if gravity gets thinner to cover more area.
We can use this painting analogy to hypothesize how gravity would work in higher dimensions. Double the radius of a four-dimensional ball and the surface area gets eight times larger. Thus, in a four-dimensional universe, we'd expect gravity to fall by a factor of eight when doubling our distance from the sun.
When we do the math, something surprising happens in more than three dimensions. For hypothetical planets to remain in stable orbits around their hypothetical sun, they'd need to travel at pinpoint speeds in precise circles. Even the tiniest variation and they'd fly off into space or spiral down to a fiery death. With such stringent restrictions, the possibility of finding solar systems or galaxies forming in such universes would be out of the question.
The situation's different in the singularly special case of three dimensions. Here, the orbital speed of a planet and the inward pull of gravity perfectly balance one another. Planets aren't limited to traveling in perfect circles, but to any number of ellipses. Give a planet a little push, or even a rather big one for that matter, and it will settle into a new, stable, elliptical orbit.
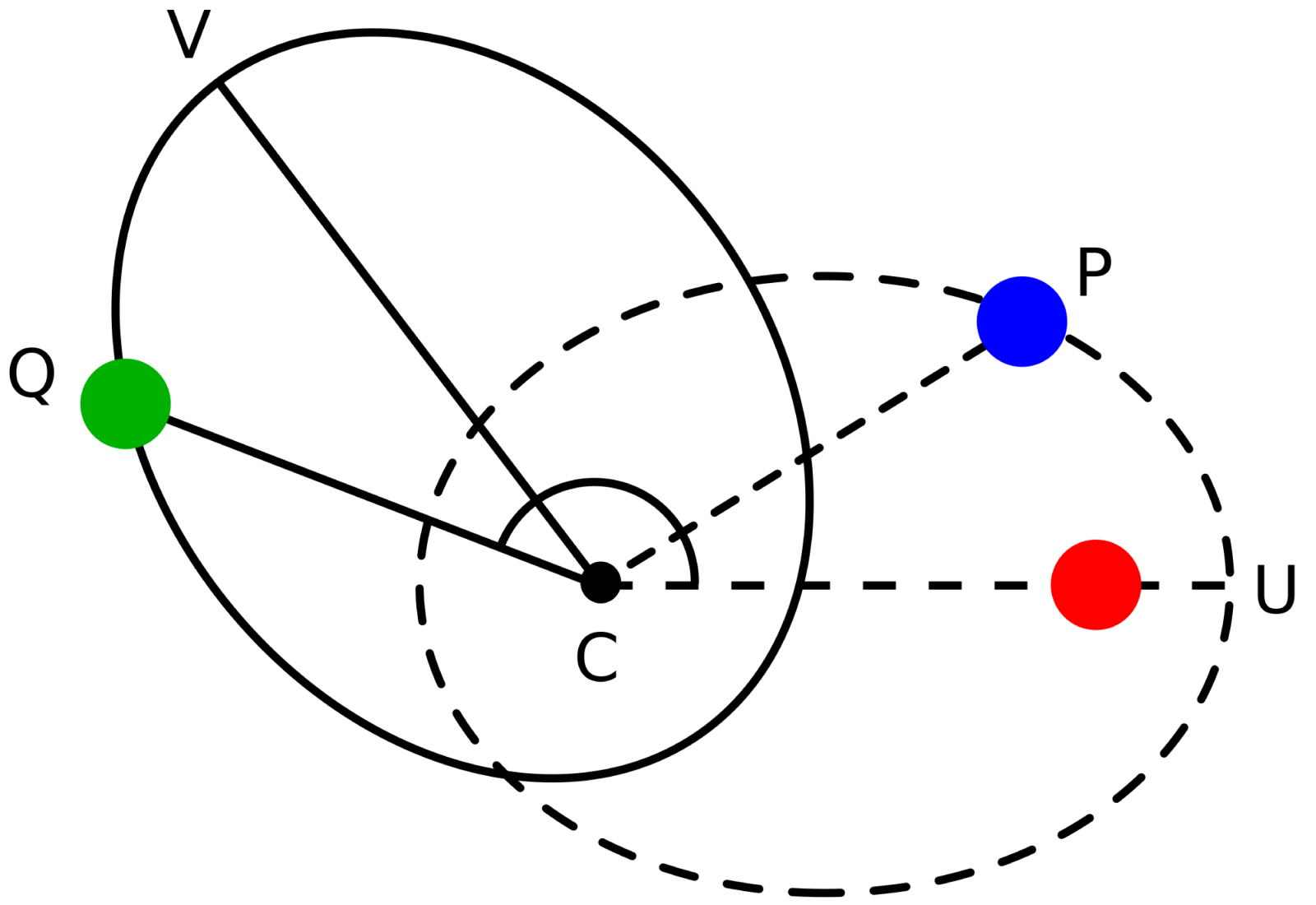
Diagram Illustrating Kepler's Laws. Photo Credit: Wikimedia
So does this mean we find ourselves living in three dimensions because any other number wouldn't work? To some, the answer is yes, and other arguments have been proffered suggesting a universe of three dimensions really is special. As for myself, reading Ehrenfest's paper simply made me smile. I'll leave you to ponder the metaphysical ramifications.
I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
Physicists developing string theoretic models of the universe postulate more than three physical dimensions, but those beyond three are typically small and unobservable.
P. Ehrenfest. "In What Way Does It Become Manifest in the Fundamental Laws of Physics that Space Has Three Dimensions?" Proceedings of the Amsterdam Academy20, 1918, pp. 200-209. See also: www.dwc.knaw.nl/DL/publications/PU00012213.pdf. Accessed December 6, 2016.
This episode was first aired on December 8, 2016