Today, math and storytelling. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

Storytelling is an art, but it's also a science. Writers speak of the dramatic arc of a storyline: the way in which a story unfolds. There are many ways to frame the structure of storytelling, but one of the simplest and most enduring is to focus on three basic elements: the beginning, the middle, and the end. And though many people don't realize it, this is how mathematicians tell their stories. 

All stories open against the backdrop of things we're familiar with. A city council meeting. A newly elected major. We bring with us a basic knowledge of what they do. Similarly, mathematicians start their stories assuming we already know things about equations and numbers, integrals and derivatives.

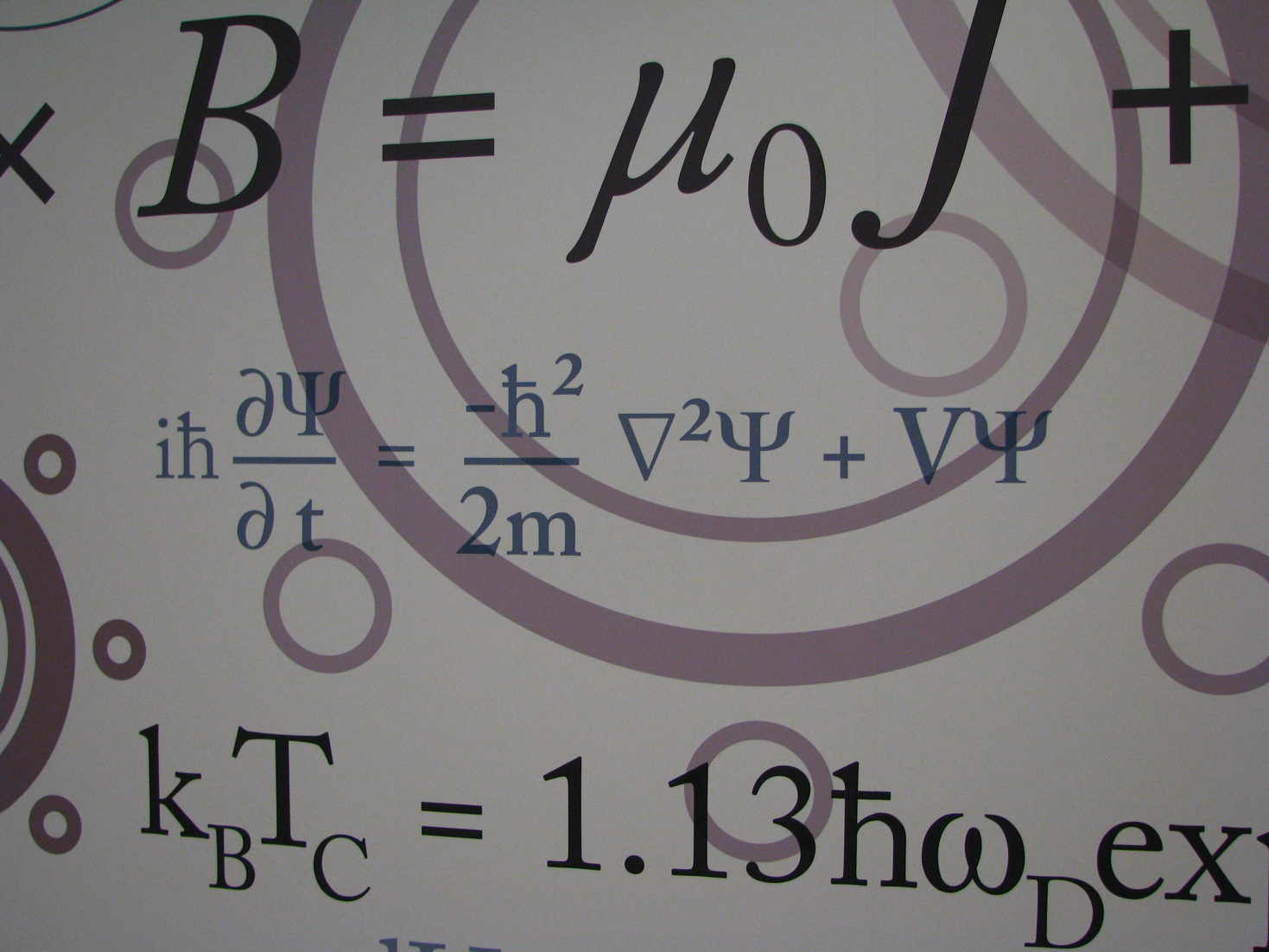
Schrödinger's Equation. Photo Credit: Flickr

The beginning of a story introduces us to basic facts about the characters. The mayor's a childhood friend of the district attorney. Some members of the council want to thwart legislation the mayor favors. In math, these are known as lemmas -- ideas that may need some explaining but that we can agree upon at the outset.

With necessary lemmas out of the way, we're ready for the middle, where the real action occurs. In math, this is the theorem. The theorem's proof may have many twists and turns. A leading councilmember is killed. Members of the city council may belong to an organized crime ring. The action rises to a climax as the villains are rooted out and the mayor emerges victorious.

The end of the story brings closure, maybe even a new surprise. Perhaps the district attorney was part of the crime ring. In math, these are known as corollaries.

When Andrew Wiles stood before an audience in 1993 and presented a proof of Fermat's last theorem, one of the most famous unsolved problems of all time, it wasn't as a theorem, but as a corollary. Why? Well, the real meat of the story was Wiles' proof of the "modularity theorem for semi-stable elliptic curves." Fermat's "corollary" proved an interesting byproduct of this broader, more enlightening theorem. The irony wasn't lost on the audience, though no one would have argued otherwise.

Like all stories, those told by mathematicians are judged by their quality. How well does the story come together as a whole? Could it be improved? But most importantly, what does the story teach us? Admittedly, reading math is an acquired taste. But for those with an interest it's worth the effort, providing a glimpse of magnificent treasure lying just over the rainbow.

Full featured double rainbow in Wrangell-St. Elias National Park, Alaska. Photo Credit: Wikimedia Commons

I'd like to end this episode with a corollary, or rather the Chorallaries, an a cappella group from a well-known engineering school.

I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.

(Theme music)

For related episodes, see FERMAT'S LAST STAND and YUTAKA TANIYAMA AND THE TANIYAMA-SHIMURA CONJECTURE.

Dramatic Structure. From the Wikipedia website: https://en.wikipedia.org/wiki/Dramatic_structure. Accessed October 26, 2016.

Fermat's Last Theorem. From the University of Saint Andrews MacTu-tor History of Mathematics Archive: http://www-groups.dcs.st-and.ac.uk/history/HistTopics/Fermat's_last_theorem.html. Accessed October 26, 2016.

This episode was first aired on November 3, 2016