Gravity Train
by Andrew Boyd
Today, slip sliding away. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
It's a wonderfully ingenious idea. Robert Hook first proposed it to Sir Isaac Newton, and it's been tossed about ever since.
Imagine carving a tunnel from Houston to Dallas — a straight tunnel about two-hundred miles long. Standing at the entrance in Houston, we'll see that the tunnel slopes slightly downhill; about three degrees — a very gentle slope. Interstate highways aren't considered steep until they're about twice that. Standing at the exit in Dallas we'll also see a tunnel that goes downhill with the same slope — upward if we're coming out of it.
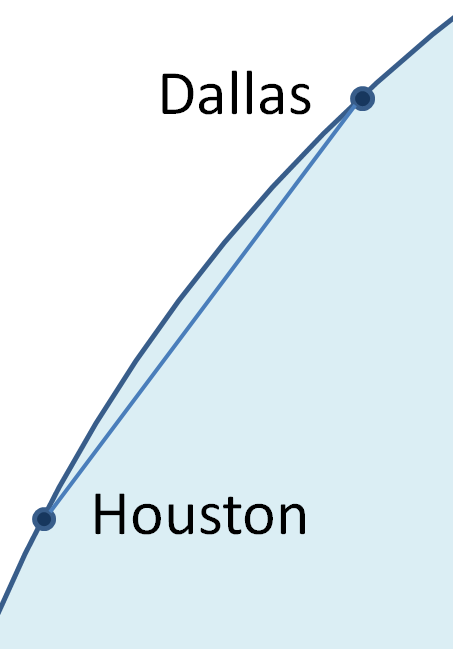
Here's what we'll do. We'll lay train track through the tunnel. Since the tunnel slopes downhill, we don't need an engine to get a train started at the station in Houston. We can just let gravity do the work. Gravity will cause the train to accelerate downhill until the middle of the tunnel, at which point it will decelerate as it rises to the other end. And by the conservation of energy, it will come to a stop just as it arrives in Dallas. We've traveled from Houston to Dallas using nothing but gravitational energy.

At its deepest, the tunnel is one and a half miles underground. At its fastest, the train travels five-hundred miles per hour. And the length of time we're riding? Just over forty-two minutes.
What happens if we build a longer tunnel, say, from Houston to Paris? The tunnel is steeper and deeper, reaching as far as 750 miles below the earth's surface. The train also travels faster, with a top speed of over 10,000 miles per hour — faster than a speeding bullet. And the time we travel? Surprisingly, exactly the same as the trip from Houston to Dallas — forty-two minutes. In fact, the length of time between any two points on earth turns out to be exactly the same.
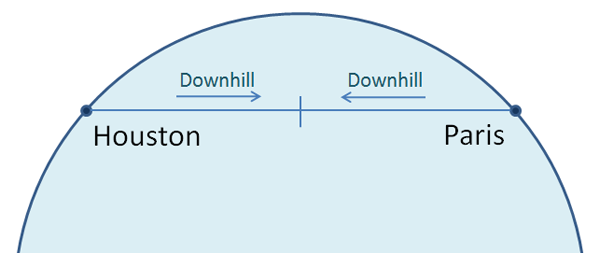
It's not hard to see why the idea keeps coming up. Unfortunately, engineering realities quickly set in.
The earth's crust is very thin. We can't tunnel through what lies below it. So about the longest tunnel that doesn't burrow beneath the crust would take us from, say, one side of Texas to the other. And that tunnel would already be far deeper than the world's deepest mines, posing all sorts of engineering challenges. But friction and air resistance are even bigger obstacles. Our mathematical abstractions assume these problems away. In reality, they'd slow the train significantly. We'd need an engine to get us back to the surface, and the trip would take much longer than forty-two minutes even with our best technology.
Still, gravity trains spark our imagination. And that's where ingenious ideas are free to flourish.

I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.
Notes and references:
Gravity Train. From the Wikipedia Web site: https://en.wikipedia.org/wiki/Gravity_train. Accessed March 29, 2011.
Gravity Train Solution. From the Purdue University Web site: https://www.math.purdue.edu/~eremenko/dvi/gravsol.pdf. Accessed March 29, 2011.
Mathematics: To Everywhere in 42 Minutes. Time Magazine. February 11, 1966.
Special thanks to illustrator and Engines listener Fredric Winkowski for the illustration of the gravity train. The picture of the train is from a Web site of the U.S. Department of Transportation. All other pictures are by E. A. Boyd.
