Today, fame that wasn't. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

When Andrew Wiles proved Fermat's last theorem he carved his name in the annals of history. After 350 years of trying but failing to find a proof, it wasn't just the mathematical community that was captivated - so, too, was the popular press. "Long Time Math Mystery Reported Solved" read the Los Angeles Times. So why, we're led to ask, was Pierre Wantzel's proof of two equally famous results completely overlooked?

To set the stage we need to travel back some 2500 years to the age of classical Greek mathematics. Geometry held a special fascination for the Greeks, especially questions about what could be drawn using only a compass and straightedge. Even today, compass and straightedge constructions remain part of the educational common core.

Compass and Straightedge Construction   Photo Credit: Wikipedia

Bust of Pythagoras in the Vatican Museum   Photo Credit: Wikimedia

Among the most famous problems the Greeks failed to solve were the doubling of a cube and the trisection of an angle. The doubling of a cube entails finding the edge of a second cube whose volume is twice that of the first. The trisection of an angle requires finding an angle that's one-third of a given angle. No matter how they tried, the Greeks couldn't find a way to solve these problems.

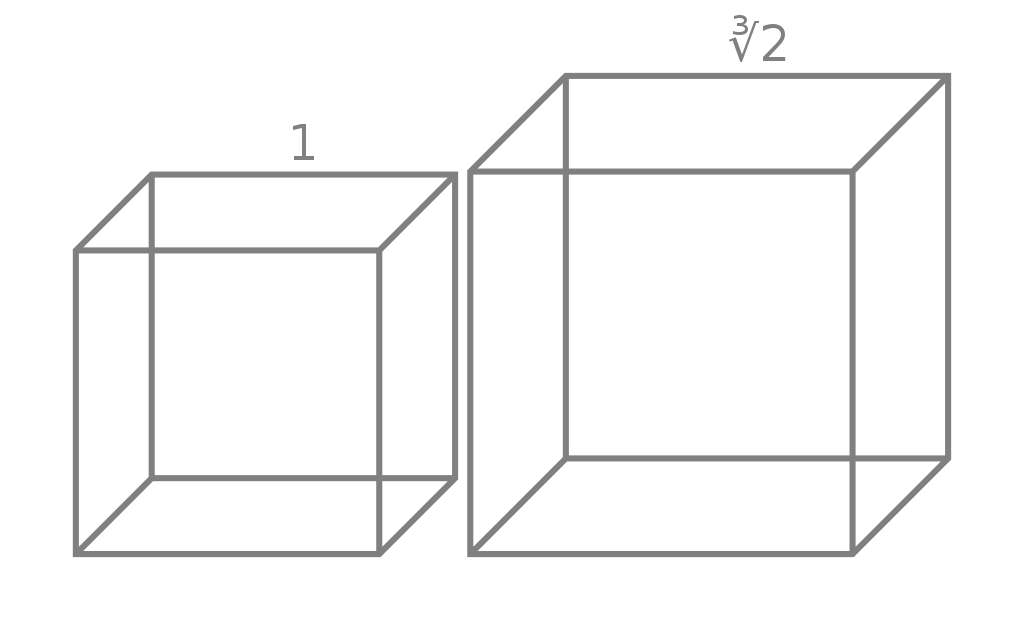
A Cube and a Cube With Double the Volume of the Original   Photo Credit: Wikimedia

Nor could anyone else. For millennia people tried again and again to double a cube and trisect an angle, but they always failed. Such was the status of these problems until 1837 when Pierre Wantzel published a proof that they couldn't be solved. Wantzel's proof appeared in a well-respected journal, and while Wantzel was only twenty-three he'd already developed a solid reputation. His paper should have brought him great notoriety. Yet it went unnoticed. The first known reference to Wantzel's paper occurred thirty-four years later, and his achievement remained virtually unknown for a century.

One reason for the delay was that as people tried to solve the famous problems they became increasingly convinced it couldn't be done. At some point, it became mathematical lore that someone had proved it impossible when in fact no one had. This situation was compounded by the fact that several highly regarded mathematicians - including Descartes, Abel, and Gauss - had made inroads into showing the problems weren't solvable. In his influential treatise Disquisitiones Arithmeticae, Gauss went so far as to claim he'd proved the impossibility result. But he then proceeded to announce that in the interest of brevity he was omitting the proof. Gauss was a mathematical giant, but he was known for making such statements to claim priority. However, no proof, no credit.

Wantzel drifted into obscurity, never achieving his potential. In generally poor health, he slept and ate irregularly and was known to misuse caffeine and opium. He died at the age of only thirty-three. While he didn't receive acclaim in his lifetime, Wantzel willfind his name etched in the annals of history.

I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.

(Theme music)

Gina Kolata. "At Last, Shout of 'Eureka!' In Age-Old Math Mystery." New York Times, June 24, 1993. See also: www.nytimes.com/1993/06/24/us/at-last-shout-of-eureka-in-age-old-math-mystery.html. Accessed July 16, 2018.

"Longtime Math Mystery Reported Solved." Los Angeles Times, June 24, 1993. See also: http://articles.latimes.com/1993-06-24/news/mn-6630_1_french-mathematician. Accessed July 16, 2018.

Jesper Lützen. "Why Was Wantzel Overlooked for a Century? The Changing Importance of an Impossibility Result." Historia Mathematica 36, no. 4 (2009): 374-394. See also: www.sciencedirect.com/science/article/pii/S031508600900010X?via%3Dihub. Accessed July 16, 2018.