Non-Constructive Proofs
by Andy Boyd
Today, knowing without knowing what. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Suppose there are 367 people in a room, and I ask you the following question: do any two people in the room share a birthday? There are a couple of good ways to approach the problem, and the answers they give are quite different in an important way.

A room full of people Photo Credit: Flickr
You could begin by polling everyone to determine their birthday, then looking to see if any two match. That's not too difficult, but it does take time.
Alternatively, you could reason as follows. There are only 365 days in a year - 366 if you consider leap years. The room has 367 people in it. Since there are more people than there are days in the year, at least two people must share the same birthday. Arguing in this way we're using what's known as the pigeonhole principle - the observation that if there are more pigeons than pigeonholes - in our case, more people than days of the year - at least two pigeons must share the same hole.

Too Many Pigeons Photo Credit: Wikimedia
But let's look more closely at the two approaches to the birthday question. In the latter case, using the pigeon hole principle, we can argue that two people have the same birthday, but we don't know who those two people are as we did in the first case. It's an example of what mathematicians call a non-constructive proof. In a non-constructive proof, we infer an answer without constructing an example that proves our case.
Non-constructive proofs are important in, of all places, online shopping. Online shopping requires encrypting credit card numbers which in turn depends on facts about prime numbers - numbers that are not the product of two other numbers. The key question for encryption boils down to this: given a very large number, is it prime, or isn't it?
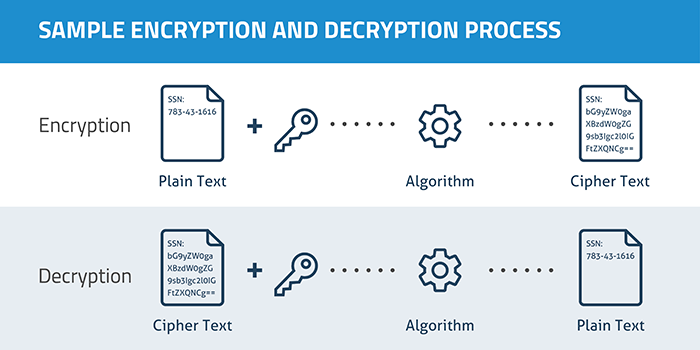
Encryption Photo Credit: Wikimedia
Well, we could start by looking for an example of two numbers that, when multiplied together, equal our large number. If we do, our large number isn't prime. If we don't, it is. But let's think about that. For the large numbers we want to test, this brute force method could take centuries.
Fortunately, due to creative thinking on the part of mathematicians, we know simple, fast methods to check if a number is or isn't prime. They don't give us example multipliers when a number isn't, but we don't care. We just want to know: prime, or not prime? And thanks to these methods, the world of online sales keeps humming right along in a way it otherwise wouldn't.
Non-constructive proofs are important instruments in the mathematical toolbox. They're often quite satisfying, knowing something is true without knowing an example that makes it true. And they can be frustrating when you need an example. A non-constructive proof teases you, telling you what you want is out there, but leaving you to find it some other way. Above all, non-constructive proofs give us yet another wonderful way in which to discover things about our world.
I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
Present encryption algorithms rely on more than simply testing if a large number is prime, but upon finding large prime numbers. However, the most efficient algorithms for finding large prime numbers rely on generating a list of potential candidates then testing them until a prime number is found. Many of the algorithms are quite creative without being overly complicated.
For related episodes, see THE PIGEONHOLE PRINCIPLE and THEORY AND ENCRYPTION.
Primality Test. From the Wikipedia website: https://en.wikipedia.org/wiki/Primality_test. Accessed December 19, 2017.
Generating Primes. From the Wikipedia website: https://en.wikipedia.org/wiki/Generating_primes. Accessed December 19, 2017.