Multiples of Nine
by Andrew Boyd
Today, the creativity in all of us. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Years ago a 14-year-old friend of mine informed me that we were "reversed ages." I wasn't sure what he meant until he pointed out that I was 41, so that the digits in our respective ages were reversed -- one-four, four-one. My friend is autistic and often observes these kinds of details, so it seemed a mere anomaly until he pointed out that we would also be reversed ages when he was 25 and I was 52, and then again when he was 36 and I was 63.
This was his way of saying the process repeats every 11 years, and a little thought shows why. Adding 11 to a two-digit number increases each individual digit by one. Try it on paper and you'll see exactly how it works.
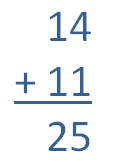
Photo Credit: Andy Boyd
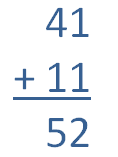
Photo Credit: Andy Boyd
So the fact that reversed ages will repeat every 11 years wasn't especially insightful. Had the story ended there, I probably wouldn't have thought any more of it. But my young friend continued with the revelation that at his next birthday he'd be reversed ages with a favorite uncle.
Intrigued by his insight, I began to wonder if some deeper mathematical structure lay behind the problem. Once started, the process repeats every 11 years, but what gets it started? Is there some special condition that leads to this two-digit two-step, or do we all share reversed ages at some time or another?
When pondering the idea driving to and from work led nowhere, it occurred to me that I should've asked the source of the insight to begin with. When I again saw my friend, I asked him why? What made people have reversed ages? His reply was remarkably simple, to the point, and seemingly out of the blue: "Multiples of 9."
At first I wasn't sure what to think. Neither 14 nor 41 is a multiple of 9. But then it hit me. Their difference, 27, is. And that turns out to be the key to reversed ages. When two people share an age difference that's a multiple of 9, they will find the digits in their ages periodically reversed. When the age difference is not a multiple of 9, they will never experience reversed ages.
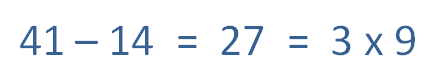
Photo Credit: Andy Boyd
Autism is a perplexing condition. Brought into the national spotlight by Dustin Hoffman and Tom Cruise in the Oscar-winning film Rain Man, autistics frequently demonstrate normal or exaggerated abilities in some areas while performing far below their peers in others. An autistic child may spell complicated words without difficulty, yet have trouble putting together basic sentences. The rules of social interaction can be learned, but the nuance of social interaction will forever remain an enigma.
My friend exhibited uncommon creativity by connecting reversed ages to multiples of 9. By thinking differently, he observed something delightful about numbers. But even more, he reminded us that there are no rules governing imagination and inventiveness; that by "thinking differently," we're all capable of remarkable feats of ingenuity.
I'm Andy Boyd, at the University of Houston, where we're interested in the way all kinds of inventive minds work.
(Theme music)
This episode is an updated version of episode 1748.
Those with specific interests in autism should check the Autism Online Support Group.
Items (1) and (2) below demonstrate the multiples of 9 property -- that two people will periodically have reversed ages if and only if their age difference is a multiple of 9. The remaining items serve as challenges for the mathematically adventurous.
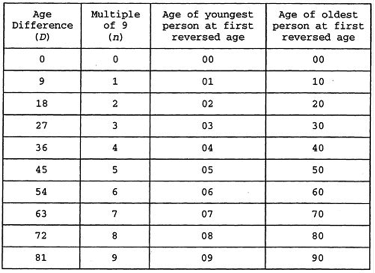
- We start by showing that two people with an age difference that is a multiple of 9 will at some point have reversed ages. It turns out that if the age difference is D, and D = 9 x n, then reversed ages are first observed when the younger person is n years old. For example, suppose the age difference between two people is D = 27 years. Then 27 = 9 x 3, making n = 3. When the younger person turns 03, the older person turns 30, and the digits are reversed. Every 11 years thereafter until the older person has a three-digit age (should she be so lucky), the two people will have reversed ages. A proof can be found in the following table for age differences up to 81.
- We next show that whenever two people have reversed ages, their age difference must be a multiple of 9. First, write the number representing the age of the older person as ab, where a is the first digit and b is the second digit. The age of the older person is then (a x 10) + b, just as the number represented by the digits '83' is (8 x 10) + 3. The age of the younger person is represented by ba, and the age is (b x 10) + a. Subtracting the ages yields [(a x 10) + b] - [(b x 10) + a] = (9 x a) - (9 x b) = 9 x (a - b). Not only is the number a multiple of 9, it is 9 times the difference of the two digits. 83 - 38 = 45 = 9 x (8 - 3).
- Consider any number with increasing digits; for example, 1256, 367, or 245,689. Any such number, when multiplied by 9, has the property that the sum of the digits in the result must be exactly 9. 9 x 1256 = 11,304, and 1 + 1 + 3 + 0 + 4 = 9. This general property is easy to prove. Write any number with, say, 5 digits as abcde, where a < b < c < d < e. Rather than multiplying by 9 directly, multiply by (10 - 1); that is, multiply the number by 10, which simply adds a 0 to the end of abcde, and then subtract abcde. Add up the digits of the result.
- The reversed ages property holds for number systems that use a base other than 10. Let B be the base of a number system. Prove that two people will share reversed ages if and only if their age difference is a multiple of B - 1, and that the period for reversed ages once they get started is B + 1. Hint: Replicate the arguments in items (1) and (2).
- It turns out that for any two numbers that have reversed digits, not just two-digit numbers, the difference is always a multiple of 9. In fact, the result is true of any two numbers made up of the same set of digits! For example, consider the number 736,253. The number 236,735 consists of the same set of digits, but rearranged. The difference between these numbers is 736,253 - 236,735 = 499,518 = 9 x 55,502. Show that the difference between any two numbers made up of the same set of digits is always a multiple of 9. Hint: Pick a number with, say, 5 digits and express it as abcde. Write the number as (a x 10,000) + (b x 1000) + (c x 100) + (d x 10) + e. Do the same for any rearrangement of the digits, and take the difference. Along the way, show that the difference of any two powers of 10 is a multiple of 9. Expand the argument to an arbitrary number of digits.
- Item (5) tells us that when two numbers have reversed digits, the difference will always be a multiple of 9. However, for any difference that is a multiple of 9, is it always possible to find two numbers with this difference that have reversed digits? If so, then we have shown the reversed ages property for all numbers, not just for the two digit ages of items (1) and (2). The table in item (1) hints at the problem. Up to a difference of 81 = 9 x 9, it is easy to find an age at which digits first become reversed. However, the process breaks down at 90 = 9 x 10. Following the same logic embodied in the table, it should be that when the younger person is 10 and the older is 100 the ages will be reversed. But this is not the case. 010 is not 100 reversed. Are there reversed numbers that have a difference of 90? Yes, quite a few, including 1101 and its reversed counterpart. When the older person reaches an age of 1101, the younger person will be 1011. What if the age difference is 189 = 9 x 21? In this case reversed ages are achieved when the older person reaches 1090 and the younger person is 0901. Question: for any difference that is a multiple of 9, is it always possible to find two numbers with this difference that have reversed digits? The author (A. Boyd) has not worked out the answer.
This episode was first aired on May 25, 2016