Stereotomy
Today, math and masonry wed, and they give birth to the trumpet squinch. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
The Roman arch seems pretty straightforward -- just a two-dimensional stack of stone wedges. But each stone has to be pre-cut in that wedge shape. And those stones have to accommodate a thin, uniform layer of mortar. Well-cut blocks typically provide for exactly a sixteenth of an inch of mortar between them.
Medieval masons took stonecutting into a whole new dimension. From the 10th to the 13th centuries, Arabic and European architects bent masonry into remarkable forms -- complex rib-work on the roofs of vaults, helical stairways, arches intersecting at strange angles. They did it all without any formal geometry. Geometry was central to medieval scholasticism, but it was the study of logic -- not a means for making things. Yet masonry cried out for geometric technique. Shaping stones to these complex forms is called stereotomy, and that means solid-cutting.
By the 13th century, masons began inventing their own approximate geometry to describe stonecutting. The glorious age of Gothic cathedrals was ending just as masons began writing down formal means for making them. By the time a new architecture emerged in the 16th century, printing presses had put Euclid's geometry into the hands of a broader public. Now exact geometrical methods helped to drive architecture.
16th-century architects started using precise intellectual apparatus to design magically spatial forms: barrel vaults, biased arches, helicoids, and something called a trumpet squinch. A trumpet squinch is a conical arch that flows smoothly out of two walls that meet in a corner. It's a support to hold the floor above, and it's a beautiful complicated shape. Just imagine trying to cut the stone blocks that can be piled into such a form. Actually, the late 16th century was giving birth to two new institutions. One was modern mathematical analysis, and the other was the wonderfully fluid shape of baroque architecture.
But the new science of architectural stereotomy drove design for only a century. It gave too much latitude to designers. When mid-17th-century architects went back to the restrictive purity of classical lines, the people who did mathematical stereotomy became hired help. By the middle 1600s, the brief, intimate bond between mathematics and architectural design had ended; and so too had its hold on our imagination.
Mathematics and architecture went their separate ways until they were rejoined in the 19th century. Then they gave us such wonders as the Crystal Palace, the Brooklyn Bridge, and the Eiffel Tower. Then they reminded us how invention is always born from a wedding of different ideas.
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
Sanabria, S.L., From Gothic to Renaissance Stereotomy: the Design Methods of Philbert de l'Orme and Alonso de Vandelvira. Technology and Culture, Vol. 30, No. 2, 1989, pp. 266-299.
This episode has been greatly revised as Episode No. 2746.
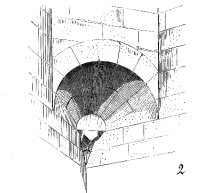
(From Dictionnaire Raisonne de L'ARCHITECTURE, MDCCCLXVIII)
Actually, the complicated Trumpet Squinch (pictured above) was already to be found in medieval cathedrals. It underwent refinement in the baroque period