The Saint Petersburg Paradox
by Andrew Boyd
Today, a paradox for the generations. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Eighteenth century mathematician Daniel Bernoulli looked at his equation and saw a problem. The math was simple. It was the implications about human behavior that had him puzzled.

Portrait of Daniel Bernoulli (1700-1782) Wikipedia Image
Bernoulli introduced his problem in a journal of the Imperial Academy of Science of Saint Petersburg, after which it came to be known as the Saint Petersburg Paradox. And like many good paradoxes it involves a game of chance. It's a great game — you're guaranteed to win money. The only question's how much.
I'll start the game by putting two dollars in a pot. Next, I'll flip a coin. If the coin comes up heads, you get the two dollars and the game's over. However, if the flip is tails, I'll double the amount in the pot and we'll flip again. That's all there is to it. Heads, you win what's in the pot. Tails, and I double the pot. It's truly a case of heads you win, tails I lose. So to be fair, I'm going to add a small twist. I'm going to charge a price to play the game. And here's the question: what price would you be willing to pay?
Let's think about it. You're guaranteed to win at least two dollars, so presumably you'd be willing to pay at least that much to play. But there's a chance you could walk away with hundreds — even thousands. Would you be willing to pay five dollars? Ten dollars? More?
With a very simple calculation, the mathematician Bernoulli pointed out the unsettling fact that no matter what the price to play, the expected value of winning is in your favor. Whether I asked a hundred dollars or a thousand or any other amount, the game is fairer than any game you'll find in a casino. But if I asked a price of a million dollars, would you pay to play? I imagine not.
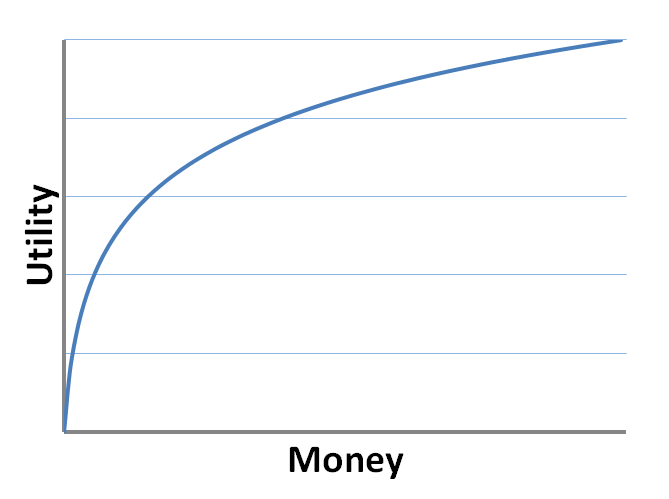
And that was Bernoulli's point. Even favorable bets aren't always perceived as good, something that was implicit in much of the early work on games of chance. Bernoulli reasoned that winning $100 when you're flat broke means more than winning $100 when you have vast sums stashed in your bank account. Our perceived value, or utility, of additional money decreases the more we have.
It's a common sense idea, but Bernoulli formalized it in the language of mathematics. And the concept, known as decreasing marginal utility, is now as fundamental in modern economic theory as supply and demand curves. And as a result the Saint Petersburg Paradox isn't quite as paradoxical as it once was.
But Bernoulli didn't close the book on this time-honored conundrum. Generations of scholars have contributed to the discussion, including such distinguished names as Euler, Cournot, Arrow, Keynes, Samuelson, and von Neumann. It seems there are always new and interesting ways to look at a good paradox, and new and interesting ways to explain human behavior — or, at least, to try.
I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
The expected value of a bet is the amount of money a person can expect to win 'on average.' It's calculated by multiplying the money won on each possible outcome, weighting it by the probability of that outcome, and adding the numbers together. For example, in American roulette, with 18 black numbers, 18 red numbers, and 2 green numbers ' for a total of 38 numbers in all ' a one dollar bet on black has an expected value of
(18/38) x $1 + (20/38) x (-$1) = -$2/38
which implies that on average you can expect to win -$2/38 per $1 wagered.
Recognizing that the probability the first head comes on the first coin toss is 1/2, the first head on the second toss is 1/4, the first head on the third toss is 1/8, and so on, the expected value of the money a person will win from the game outlined in the essay is
(1/2) x $2 + (1/4) x $4 + (1/8) x $8 + ...
= 1 + 1 + 1 + ...
= ∞
The payouts rise so quickly that the expected value of the money won is infinite. Thus, no matter what finite amount you pay to play the game, the expected value of the winnings remains infinite.
D. Bernoulli (1954) [1738]. 'Exposition of a New Theory on the Measurement of Risk.' Econometrica, 22, pp. 23'36.
B. Hayden and M. Platt (2009). 'The Mean, the Median, and the Saint Petersburg Paradox.' The Journal of Judgment and Decision Making, 4(4), pp. 256-272.
R. Martin. The Saint Petersburg Paradox. From the Stanford Encyclopedia of Philosophy website: http://plato.stanford.edu/entries/paradox-stpetersburg/. Accessed December 2, 2014.
This episode first aired on December 3, 2014.