Today, we're put on hold. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

It's happened to all of us. We call with a question about a bill or to get help with a new purchase, and we're shunted to a world of unfamiliar music and a voice that intermittently tells us: "All operators are busy. Please stay on the line and your call will be answered by the next available agent."

Why can't companies simply hire enough people to answer our questions?

A Call Center (Wikipedia Image)

In 1908 a young man by the name of Agner Erlang was faced with a similar question. A student of mathematics, Erlang was persuaded to join the Copenhagen Telephone Company as head of its newly established technical laboratory. The lab faced an important question: how many switchboards and operators should the phone company provide?

Agner Erlang (Wikipedia Image)

Erlang was a private man, quiet and well read, though in the company of others he was described as full of humor and wit. He lived a frugal lifestyle that gave him the means to help the needy, which he seemed most happy to do. And as he observed the working of the switchboard operators, Erlang put his math to work. First, he had to describe the random arrival of callers in the language of mathematics. He then needed a similar description of how long callers spent on the phone. Armed with these mathematical descriptions of the randomness, he developed the tools needed to answer all sorts of questions, questions like: if 100 people operate 100 switchboards, what's the chance everyone who calls gets through? Erlang could connect the number of switchboards and operators to very specific levels of service. His 1909 paper, 'The Theory of Probability and Telephone Conversations' is generally regarded as the first paper in the field of queuing theory — the study of waiting lines.

Telephone Operators Operate Switchboard at Potsdam Conference (Wikipedia Image)

Erlang's work was soon used by companies around the world. Not just telephone companies, but banks, post offices, and anywhere else a line could form. Queuing theory remains an active area of research as we study ever more complicated systems of waiting lines. And not just waiting lines of people, but all sorts of things, like the parts and components required to make a jet aircraft. And the same math employed over a century ago by a modest, bookish Dane is still used to model communications systems world over.

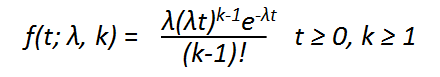
Erlang Distribution 

Including call answering centers. It's important to realize that Erlang's work describes the precise relationship between waiting and the number of phone agents. What Erlang's work doesn't do is prescribe how long the wait should be. Companies look at the tradeoff between how long we wait and the cost of more agents and make their own decisions.

But thanks to the work of Erlang and many others since, companies are in a position to make informed decisions — and to keep us callers better informed about our waits. Still, that comes as little solace when the digital voice on the end of the line intones, "your expected waiting time is now 17 minutes."

I'm Andy Boyd at the University of Houston, where we're interested in the way inventive minds work.

(Theme music)

Advances in Queueing Theory, Methods, and Open Problems. J. Dshalalow, ed. CRC Press, 1995.

Agner Krarup Erlang. From the website of the MacTutor History of Mathematics Archive, Saint Andrews University: http://www-history.mcs.st-and.ac.uk/Biographies/Erlang.html . Accessed September 21, 2014.

This episode was first aired on September 25, 2014.