Today, The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Max Lorenz was a doctoral student at the University of Wisconsin in 1905, when he published a paper titled: Methods of measuring the concentration of wealth. He included a graph that summed the income against the population from poorest to richest.
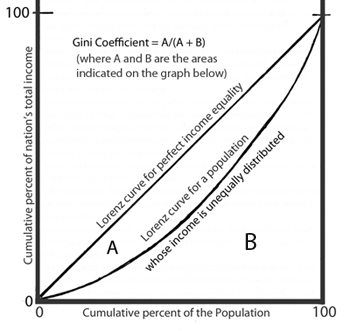If everyone in a country had the same income, the line would be straight. Great disparities between rich and poor give a deeply concave line. It was a neat way to show the pattern of income. Lorenz's curve certainly didn't bring in all the factors. But it drew attention to a terribly important issue by displaying it in an obvious way. And it raised all kinds of questions.
For example, is perfect equality of income desirable? Lorenz curves for the old communist countries were very straight. Those countries regulated wages, but they made some people wealthy by providing privileges. Lorenz curves didn't show that grim back-story.
On the one hand, when we have incentives for doing more and doing better, income cannot stay uniform. But a subtle mathematical catch arises. It's this: A society that offers great access to opportunity tends toward greater equality of income. More people will find more ways to create and share wealth.
That might seem counter-intuitive -- the fact that true equality of income is not a product of leveling by the state. It's a product of human enterprise. Access means that a Horatio Alger child need not stay poor. And yet ... well, things are never really quite what they seem.
Let's look at equality of income in real countries: One common measure is the ratio of earnings of the top and bottom ten percent of the people. In the US and Uganda, that ratio is sixteen. In Canada and Switzerland it's only nine. American incomes are very unequal and they've been getting steadily worse for over forty years.
So, back to mathematics: The math tells us that, when it's a simple matter of having access for our potential, incomes tend to equalize. When artificial factors keep high incomes high, and low incomes low, we are in trouble.
As I write in 2011, Democrats and Republicans both claim to know how to fix our poor economic situation. Yet inequality has steadily risen under both parties. So maybe I should add my own silver bullet to the many silver bullets flying about us today.
If economic woes and inequality of income are wed, let's find means for reducing inequality. It's both the problem and the main symptom. The gap between our rich and our poor now matches countries like Mali, Cambodia, and Nigeria.
We are a smart, energetic, creative people. We can invent our way out of this situation just as we've invented better health and better transportation. Find a way to get problem solving out of the political arena and I promise you. We can lick this one as well.
I'm John Lienhard, at the University of Houston, where we are interested in the way inventive minds work.
I've developed the math behind the idea of access, with two coauthors, in two places: Paul L. Meyer and I created the mathematical tool in this paper:
L. Berkley Davis, Jr. and I applied these ideas to income distribution in this paper:
Once one has plotted a Lorenz curve, one may evaluate it by dividing the area under the perfect-equality, straight-line curve by the area under the actual curve. Subtract that ratio from 1 and the result is called a Gini Coefficient. A Gini Coefficient of 1 is perfect inequality. A Gini Coefficient of zero is perfect equality. Gini Coefficients for the US and Senegal are 0.41. For Canada and France, they're 0.33. For Denmark and Japan, they're 0.25.
See also the Wikipedia pages for Lorenz Curve, Gini Coefficient, Economic Inequality, List of Countries by Income Inequality, and Income Inequality Metrics.
This episode was first aired on September 26, 2011
Wealth and poverty -- inequality of income -- side by side in Cochin, India. The Gini coefficients for India and the US are and 36.8 and 40.8. Their incomes are just a bit more equal than ours. (Image courtesy of Wikimedia Commons.)