by Andy Boyd

Today, guest scientist Andrew Boyd looks at some divine shapes. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

For many of us, the word mathematics evokes fear or, what may be worse, dread. Yet, throughout history, mathematics has often inspired awe and been the focus of mystical or religious devotion.

One alluring mathematical artifact is the collection of regular solids -- three-dimensional shapes with identical sides and corners. The cube is a regular solid. It has six identical sides, all squares. It also has eight identical corners.

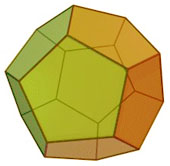
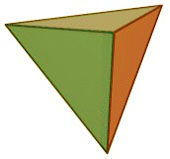The simplest regular solid is the tetrahedron, made of four identical triangles. It looks a lot like a pyramid, but has a triangle rather than a square for its base. Altogether there are only five regular solids. The remaining three are the octahedron, the dodecahedron, and the icosahedron.

The fact that there are only five regular solids can be traced to Euclid, who devotes much of the final chapter of his work the Elements to various facts about the regular solids. However, it's Plato whose name is most closely attached to these solids. Plato 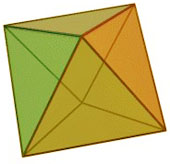associated one solid with each of the four basic elements -- fire, earth, air, and water. He reserved the fifth for the heavens beyond the stars and planets. Plato's theory of how the universe worked was so intimately connected with the regular solids that they're often referred to as the Platonic solids.

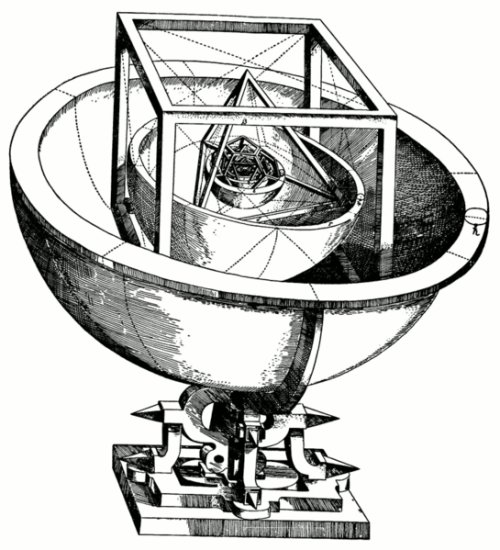
Two thousand years later, Johannes Kepler also fell under the spell of these ethereal forms. Best known for his three laws of planetary motion, Kepler's earliest published work, the Mysterium Cosmographicum, focused on how the regular solids could be used to explain the orbits of the planets. He alternately nested spheres and solids inside of one another so they all fit tightly together. This nesting was such that the relative sizes of the spheres were close to the relative sizes of the planets' orbits. (At the time, only six planets were known.)

Unlike Kepler's laws of planetary motion, which were profound insights, his nested solids idea added nothing to our knowledge of planetary orbits. It's often pointed to as an example of misguided pseudo-science. Yet both ideas stemmed from Kepler's devout conviction that God expressed himself in the beauty of nature. The planets and stars were long considered the Creator's most perfect expressions of his being. By connecting the planets' orbits with the regular solids, Kepler was elevating these mathematical forms to the level of the divine.

Today, we may not treat the regular solids with the same esteem as Euclid or Plato or Kepler, but their allure remains as strong as ever. A quick search on the Web yields hundreds of links to the regular solids, almost all with pictures, some with fancy three-dimensional renderings. Many of these Web pages are set up by individuals who simply find beauty in these shapes, and perhaps puzzle over why nature only gave us five. And I have to admit, as I stare at the stick models in my office that I made many years ago, I can't help but still smile at the elegance of their symmetry.

I'm Andy Boyd, at the University of Houston, where we're interested in the way inventive minds work.

Dr. Andrew Boyd is Chief Scientist and Senior Vice President at PROS, a provider of pricing and revenue optimization solutions. Dr. Boyd received his A.B. with Honors at Oberlin College with majors in Mathematics and Economics in 1981, and his Ph.D. in Operations Research from MIT in 1987. Prior to joining PROS, he enjoyed a successful ten year career as a university professor.  His latest book is: The Future of Pricing: How Airline Ticket Pricing Has Inspired a Revolution. (New York: Palgrave MacMillan, 2007).

For more on the Platonic Solids, see: http://math.ucr.edu/home/baez/platonic.html
or  https://en.wikipedia.org/wiki/Platonic_solid

For more on Kepler, see: https://en.wikipedia.org/wiki/Johannes_Kepler

The five Platonic solids above are displayed in the following sequence, top to bottom: The hexahedron or cube (6 sides), tetrahedron (4 sides), octahe-dron (8 sides), dodecahedron, and icosahedron. Below, see Kepler's model of the solar system with the planets riding in nested Platonic solids. (Public domain images courtesy of Wikipedia).