Jean-Charles Borda
Today, let's meet Jean-Charles Borda. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
I find it wonderfully odd -- how names outlive the people they once belonged to. I talk with younger engineers who studied in UCLA's Boelter Hall. They look at me oddly when I mention having talked with Boelter, for one does not converse with a name on a building. We in technical fields attach so many names to theorems, laws, and devices without any mental picture of the people.
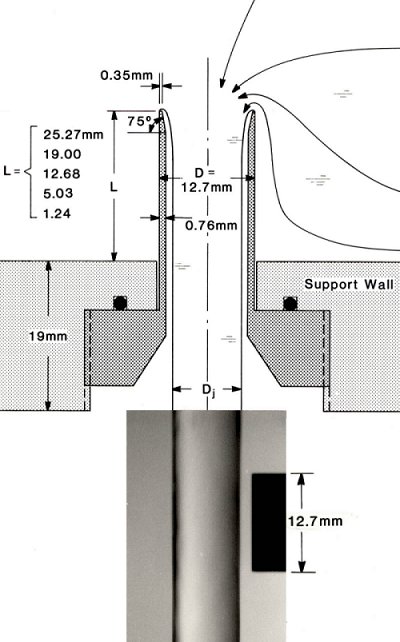
I once worked on metering orifices, and one such meter was the Borda Mouthpiece. It's a short tube inserted into the wall of a tank. Water inside does a 180-degree turn into the tube, forms a perfectly clean jet, and leaves without touching the tube walls. Elementary theory, says the jet should have exactly half the area of the tube.
That would allow the device to meter the flow very accurately; but there's a catch: Everyone who's ever tested a Borda mouthpiece has measured a flow that's high by several percent. Why? A colleague and I finally solved that riddle -- both experimentally and theoretically -- and we showed how to correct the measurement.
 Yet we did all that with no clue -- no thought -- about the person of Jean-Charles Borda. And that's a shame, because Borda was a remarkable figure. He was born of French aristocrats in 1733. After his education, he worked the rest of his life as a military engineer and as a naval officer. All the while, he did wonderfully creative scientific and engineering work.
Yet we did all that with no clue -- no thought -- about the person of Jean-Charles Borda. And that's a shame, because Borda was a remarkable figure. He was born of French aristocrats in 1733. After his education, he worked the rest of his life as a military engineer and as a naval officer. All the while, he did wonderfully creative scientific and engineering work.
At the age of 31, he was made a member of the French Academy for his work on the physics of projectiles. His studies of energy conservation laid ground for the subject of thermodynamics. He invented a new surveying instrument called a reflecting circle. He worked in the Caribbean testing new longitude chronometers.
In 1770 Borda proposed a method of voting for multiple candidates. Using the so-called Borda count, voters rank candidates from a low of one to a high equal to the number of candidates. The points are summed to name the winner. Alas, mathematical economist Kenneth Arrow later showed that, not only does a simple majority fail to produce the most desired candidate -- neither does Borda's method.
But that was still the idea of a rationalist looking for better self governance. He fought with the French in the American Revolution -- eventually put in charge of six vessels. His war ended in 1782, when the British captured him. After his release, he turned his attention to hydraulics -- and to my own Borda tubes.
Late in life, he was part of yet another rationalist cause: He served on the blue-ribbon committee that defined the meter as one ten-millionth of the distance from the pole to the equator.
So, years ago, I watched the frozen motion of perfect jets leaving inverted tubes and did not imagine the swirling creative energy behind it. I didn't dream, as I ought to have dreamt, that Borda was so much more than a name randomly attached to a device.
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
C. S. Gillmor, Borda, Jean-Charles. Dictionary of Scientific Biography, C. C. Gillispie, ed., Vol. II (New York: Charles Scribner's Sons, 1970): pp. 299-300.
W-g Dong and J. H. Lienhard, Contraction Coefficients for Borda Mouth-pieces. Journal of Fluids Engineering, Vol. 108, No. 3, Sept. 1986, pp. 377-379. To read this source on-line, Click Here.
See also: https://en.wikipedia.org/wiki/Jean-Charles_de_Borda
For more on Arrows impossibility theorem see Episode 1921, and: https://en.wikipedia.org/wiki/Arrow's_impossibility_theorem

Three Borda tubes (or mouthpieces): Borda's theory predicts the flow to be (A/2)×(2gh)1/2 (where A is the cross-sectional area of the tube, g is the gravitational acceleration, and h the liquid head in the supply tank.) But the length of the tube must be far longer than the diameter for that to be true. The shortest tube shown here gives a flow rate that is high by eight percent. It is high by about one percent for the longest tube. (JHL's scanned image)
Borda tube experiment (Dong and Lienhard.)