The Statistics of War
Today, we count our dead. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
This new year of 2002 finds us at war once again. I suppose that's why science writer Brian Hayes has chosen to talk about the books of early twentieth-century scientist Lewis Fry Richardson.
Richardson was a Quaker who quit his job as a meteorologist to drive ambulances in WW-I. After that, he decided that it was time for a cold-blooded look at war. He asked: how often do we fight, and how many people do we kill? Viewed as detached data, how do wars fit into the overall fabric of things?
He realized that, just as earthquakes and gales must be ranked logarithmically, so too must wars. His measure of the magnitude of the death toll in war was the number of digits to the right of the first digit in the number. (That's what someone mathematically-inclined would call the order of magnitude of the death toll.) Thus a war of magnitude five leaves a hundred thousand dead. World Wars One and Two were both over magnitude seven, killing tens of millions each. A conflict of magnitude one would kill only ten or so people.
Richardson was surely being provocative when he included wars of magnitude zero in his categories. That would reflect a conflict that killed only one person -- more commonly called a murder.
But, when we look at Richardson's data, we find that numbers for murders blend right in with those for war. Suppose you plotted the total number of conflicts of each magnitude. So far, the two World Wars have been the only ones of magnitude seven. That number rises exponentially as the magnitude decreases until it reaches around ten million conflicts of magnitude zero. However, the number of deaths from conflicts of any magnitude is up in the millions. So far, murders have killed about as many people as world wars have.
Richardson's background in math was strong, and he put his math to use. His was no casual exercise in data-keeping. One of his books, Arms and Insecurity, is awfully rich for the diet of anyone who doesn't have a graduate degree in math.
Yet he created a field that's being carried on by others today. And the data give us a lot to think about. Among conflicts that kill over five thousand people, most, by far, occur among neighbors. The eighteenth century, when Great Britain was strongest, was also when the world suffered the fewest wars -- about thirty each decade. In the years around the turn of the twentieth century, that worsened to nearly a hundred wars each decade. Other data show that war occurs with remarkable randomness.
In one of his book prefaces, Richardson likens his work to that of an engineer writing on dynamics. What's the connection between a book on dynamics, and engineering design, he asks? The answer is that, while dynamics won't help you design anything, you'd better not try designing any machine without knowing it.
Richardson doesn't presume to tell politicians how to stay out of war -- only that they need to understand the forces surrounding war before they tangle in it. And Brian Hayes finishes by blandly pointing out that if we ever experience a magnitude-9.8 war, that, at least, will be the one war no one will ever have to worry about afterwards.
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
Richardson, L. F., Statistics of Deadly Quarrels. (Quincy Wright and C. C. Lienau, eds.) Pittsburgh: Boxwood Press, 1960.
Richardson, L. F., Arms and Insecurity. (Nicolas Rashevsky and Ernesto Trucco, eds.) Pittsburgh: Boxwood Press 1960. (This is the source of Richardson remark that I paraphrase near the end of the episode above.)
(Each of the books above was a posthumous edition of a manuscript whose Preface Richardson had signed in 1953.)
Hayes, B., Statistics of Deadly Quarrels. American Scientist, Vol. 90, No. 1, January-February, 2002, pp. 10-15.
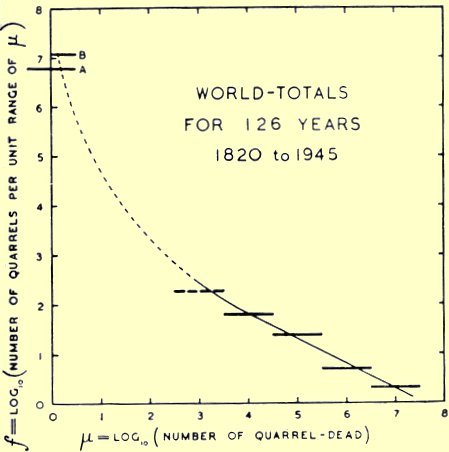
Richardson's representation of the number of conflicts of each magnitude compared with the number that died in each. (From Statistics of Deadly Quarrels)