Today, the forgotten lecture in your math course. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

What engineer doesn't remember dozing off in math class when the professor took up existence and uniqueness? Those words have a special meaning in math. Not all problems have solutions, and, if they do, there might be more than one. A problem with no solution isn't much use. And more than one solution puts us in a quandary.

Engineering students grow impatient with those issues because equations that reach their classrooms almost always do have unique solutions. Suppose, for example, a fast-moving car hits a turn. It either rolls over or gets around the curve safely. It doesn't do both. We'd better get just one solution when we solve the problem. It's cold comfort if our math tells us it will both roll over and get around safely. We need to know which will happen.

Try another kind of accident. I have a long slender glass rod -- say a yard long and an eighth of an inch in diameter. I stand it, on end, on the floor -- then begin pressing downward on the top. Nothing happens, so I press harder. I finally reach a point where the rod suddenly bows outward and breaks. If I set up the math correctly, it'll tell me how much load the rod will take.

But that solution is not unique. There's another solution. It has the rod bending into an S-shape instead of simply bowing outward. More solutions also exist: a triple bow, a quadruple bow, and so on. Since the fancier failure modes take a lot more force, the rod usually collapses by simply bowing outward. We trigger that simple failure mode as we increase the load slowly. But suppose we add a greater load all at once. Then those fancy collapses actually can occur.

If you hold the glass rod by its end, high above a concrete floor, then drop it, the load is applied so suddenly that the rod will collapse in one of those wavy shapes. I once did that. The glass broke into six pieces, all the same length. The rod had been wavy as a snake when it collapsed under an enormous shock loading.

That taught me a fine lesson about the limitations of my work. Louis Pasteur once remarked that "Chance favors only the prepared mind." If I can paraphrase that, I'll say that rod taught me to expect surprise. Even when we've polished and honed our means of prediction, outcomes might still not be unique. Nature has all kinds of alternatives up her sleeve, and we'd better be ready for them.

Swiss mathematician Leonhard Euler solved the collapsing rod problem in the eighteenth century. Determinism then appeared to be the way of the world. Now the twentieth century has given us first quantum indeterminacy and then chaos theory. We struggle to create new descriptions of a reality that's not so straightforward. We once could yawn when math teachers began talking about existence and uniqueness. Now our ears prick up. For we no longer live in that simple world where only one outcome is thinkable.

I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.

(Theme music)

For some discussion of mathematical existence and uniqueness, see, e.g., Sneddon, I. N., Elements of Partial Differential Equations. McGraw-Hill Book Company, Inc., 1957, pp. 9 and 48.

For a very good account of the Euler column analysis, see: Pippard, A.J.S., The Analysis of Engineering Structures. London: Arnold, 1957; or Popov, E. P., Introduction to Mechanics of Solids. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1869.

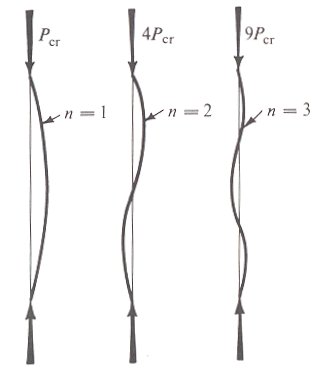
Three modes of failure of a column. (The force needed to cause a collapse rises as the square of n.)