Teaching and Ambiguity
Today, teaching and ambiguity. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
I've done classroom teaching ever since January of 1952. Yet I view teaching with vast distrust. I cannot bear to be told what I might just as well have read out of a book or, better yet, figured out myself.
One fall, long ago, I took two classes. One teacher was known for his clarity. You left his lectures with perfect class notes -- no thought incomplete, no question unanswered. The other teacher presented a wild muddle -- stray thoughts spinning about a central theme, a great sunspray of disorganized ideas. Back in my room, I rewrote each lecture as the good teacher might've delivered it. You can guess the outcome. The good teacher left me with only a clean set of notes. The would-be poor teacher enriched my life.
The subject in both classes was what mathematicians call complex analysis -- so-called imaginary numbers. One course dealt with it as math. The other course was about fluid flow. Let me offer a little background here. First, think about squaring numbers:
Two squared is four; three squared is nine; 1.4 squared is a little less than two, and so on. The square root of two has an infinite number of digits. You can never write it down with complete accuracy, but you can come close. Now ask about negative numbers. What's the square root of minus four? Square either two or minus two and you get plus four. Since we can make no obvious physical sense of the square root of minus four, we call it imaginary.
That may sound like angels dancing on the heads of pins, but like so much of mathematics, it reveals a great deal about the nature of things. Describing the motion of moving air or water is a daunting mathematical task. In the early 19th century, two mathematicians -- Cauchy and Riemann -- set up tools that were later used to explain those motions. The idea, stunning in its elegance, works like this:
We solve equations that describe both real and imaginary numbers. Then the real and imaginary pieces of the solution describe facets of fluid motion. An abstraction suddenly turns out to be very useful. That sort of thing happens all the time. Again and again, seemingly silly branches of math become mirrors of reality.
So I spent the Fall of 1956 in two classes, studying two faces of the same problem. Both classes demanded that I come to terms with alien ideas. Both classes were about things I would often put to use during my long life as an engineer. And, together, those classes taught me about the greatest abstraction of all -- the idea that one person can teach another.
That fall, I rewrote the poor teacher's notes until they looked like the notes of the good teacher. Today, I can't even remember the good teacher's name. But I think about that poor teacher every day of my life. He added as much to my mental growth as anyone, short of my parents -- against whose unexplicit and formative teaching I inevitably weigh all others.
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
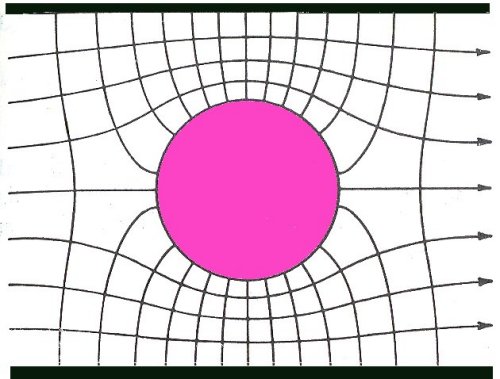
A typical example of a calculation done with the help of complex analysis: Ideal fluid flow over a cylinder between two walls (top and bottom). The lines with arrows on them represent "streamlines" or the movement of any "particle" of fluid. The lines perpendicular to the streamlines are called "potential" lines since they reflect the impetus for the motion.