Today, the mathematics of space travel. The University of Houston presents this series about the machines that make our civilization run, and the people whose ingenuity created them. 

Science fiction writers imagine that our descendants will use wormholes to travel across galaxies without using much energy. We do not yet know how to cross vast distances in a blink. However, using celestial mechanics — the mathematics that describes the motion of celestial bodies — astrophysicists have found ways of crossing space using very little fuel. 

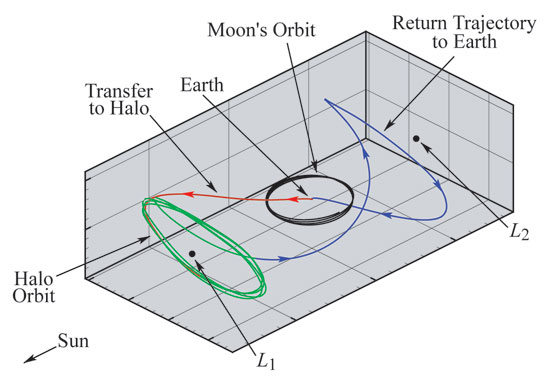
Diagram of the Genesis space mission. Photo Credit: WhyDoMath.org

To understand how this is possible, think first of the Earth and the Moon. Each exerts a gravitational pull on objects, while they spin around each other. Connect the centers of the Earth and the Moon with an imaginary line. Somewhere along this line, the pull of the Earth equals that of the Moon, but in the opposite direction. Placing a spacecraft at this point is like placing it on a knife's edge: A small nudge will break the balance of forces and send it drifting towards the Earth or the Moon. This position is called a "libration point". The mathematicians Leonhard Euler and Joseph-Louis Lagrange showed that there are five libration points in a system of two rotating bodies such as the Earth and the Moon. At these points the combined gravitational forces of the two celestial bodies give exactly the right pulls to keep an object orbiting in an unchanging position.

Two of these libration points are stable -- satellites placed at these points will remain there forever. However, the remaining three libration points are unstable, and these are key to low energy space travel. Imagine placing a marble exactly at the ridge of a saddle. The marble will roll down the ridge towards the saddle's center, but a small nudge can make it veer down either side. The unstable libration points are similar to the center of the saddle -- a spacecraft at the right position going at the right velocity travels along something like the saddle's ridge approaching the libration point. A small nudge can make it veer down either side of the saddle. If this is done just right, a path leading away from the ridge can take the spacecraft along just the orbit we want it to follow.

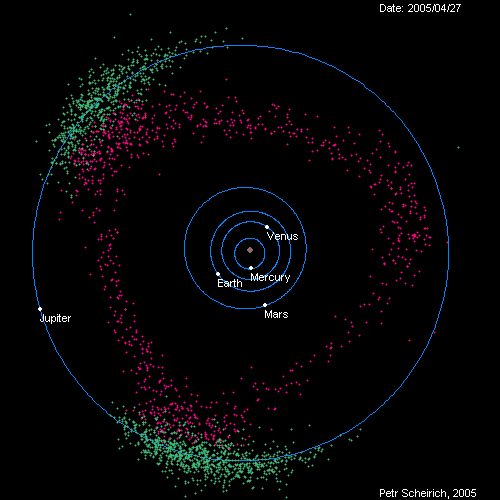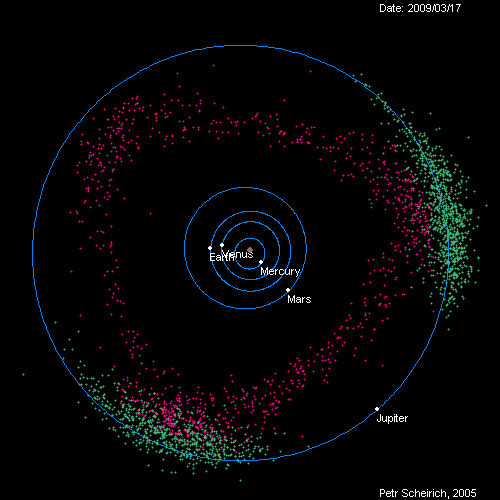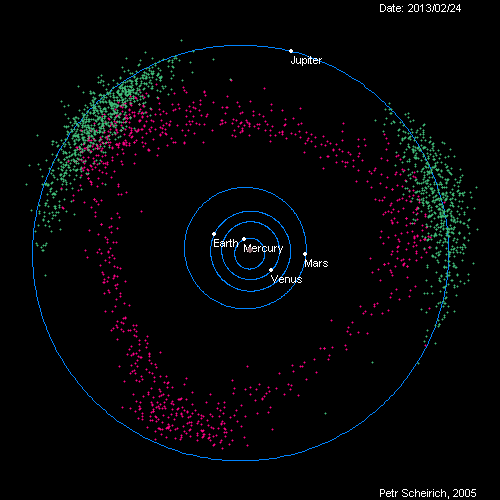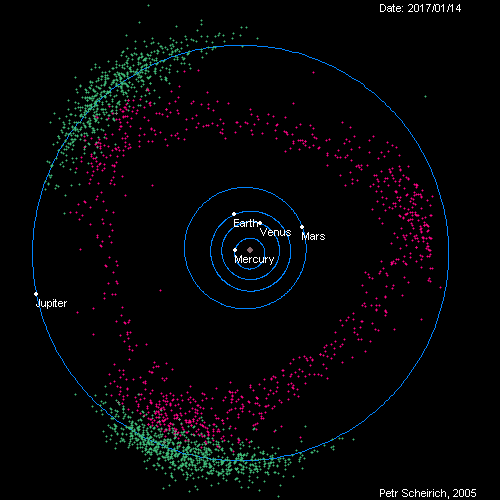
Jupiter 'shepherds' the asteroid belt, preventing the asteroids from falling into the sun or accreting into a new planet. Photo Credit: imgur

However, in the Solar System everything is in motion, so the saddles and the ridges keep spinning and swerving through space! Essential to mission design are good mathematical models of the solar system, and the computational tools to solve these models accurately.

Traveling along the resulting trajectories can take a long time. However, their benefits can be great. The spacecraft Genesis went along such a trajectory to sample the solar wind while using only a fraction of the fuel expended by similar spacecraft in the past.

For thousands of years humans have tried to understand the motion of the planets. The language of mathematics can lead to such an understanding. But mathematics has also provided much more: it has told us how to traverse the Solar system, and may some day lead us far beyond.

This is Krešimir Josić at the University of Houston where we are interested in the way inventive minds work.

(Theme music)

I am grateful to independent astrodynamics consultant Daniel Adamo, retired NASA planetary scientist Wendell Mendell, and astronaut Michael Barratt for their help in preparation of this episode.

I simplified the explanation of the trajectories between libration points here. They are in fact not straight lines, but take the form of spirals on the surface of tubes. These tubes approach closed orbits that surround the libration points. We are accustomed to the closed orbits of planets around the Sun (or any object that has mass) described by Kepler's Laws. But libration points have no mass. It may therefore be surprising that we have closed orbits around points of no mass! A discussion of the mathematics of interplanetary travel along the orbits I discussed can be found here http://www.whydomath.org/node/space/mission.html 

A number of further references, including more technical ones are provided in this article. Note that the feasibility of interplanetary missions using the same principles remains controversial.

The Wikipedia page also has an intuitive explanation of why they appear https://en.wikipedia.org/wiki/Lagrangian_point. Indeed, many asteroids can be found at the two stable libration points of the Sun-Jupiter system. These are known as the Trojan asteroids: One libration point is home to the Greek camp, while the other houses the Trojan camp. A nice picture of the Jupiter Trojans is here https://en.wikipedia.org/wiki/Jupiter_trojan.

Joseph-Louis Lagrange was an interesting figure himself. For his rich life that spanned the French Revolution and his many contributions see here https://en.wikipedia.org/wiki/Joseph-Louis_Lagrange

This episode was first aired on March 1, 2016