Simpson's Paradox
Today, paradoxical averages. The University of Houston presents this program about the machines that make our civilization run, and the people whose ingenuity created them.
In 1973 the University of California at Berkeley was sued for sex discrimination in graduate student admissions. The case looked clear cut: the university admitted only 35% of female, but 44% of male applicants to graduate programs. However, when statisticians looked at the data in more detail they found a surprise. When looking at the admission rates of individual departments, the apparent bias disappeared. Individual departments were either more likely to admit women or about as equally likely to admit women as men. At the level of individual departments women seemed to have a slight advantage over men.
This is an example of Simpon's paradox — a paradox that can affect averages whenever we combine, or pool, data. Here is another example involving two New York Yankees players, Derek Jeter and David Justice. In both 1995 and 1996 David Justice had a higher batting average than Derek Jeter. However, when we compute the batting average over both seasons, then Derek Jeter is ahead of David Justice. Again, pooling the data gives a different picture than when looking at smaller chunks.

New York Yankee Derek Jeter warming up before a game. Photo Credit: Wikimedia Commons

David Justice at the premiere of "Moneyball" Photo Credit: Wikimedia Commons
How is this possible? Let's look at the case of graduate school applicants to the University of California at Berkley. It turns out that more women applied to departments in the humanities, while men tended to apply in higher numbers to engineering and science departments. Humanities departments had fewer available slots, and rejected more applicants. Thus female applicants applied mostly to departments which admitted fewer students, whether male or female. As a result, the overall fraction of women admitted to graduate school was lower than that of men, even though women had an equal or better chance of being admitted to individual programs. A bias did exist, but it was not a bias in the rate of admissions. Rather, it was a bias in the number of women who chose to apply for graduate studies in technical fields.
Simpson's paradox can have important consequences. For example medical researchers compared a less invasive treatment for kidney stones to established surgical methods, and found the new treatment to be better overall. However, in the study the less invasive treatment was more frequently applied to small kidney stones. Since smaller kidney stones are easier to treat, this gave an advantage to the new, less invasive method. When the treatments were compared separately on small kidney stones and large kidney stones, traditional treatments proved to be more successful. Taking into account kidney stone size completely changed the conclusion about which treatment is better.
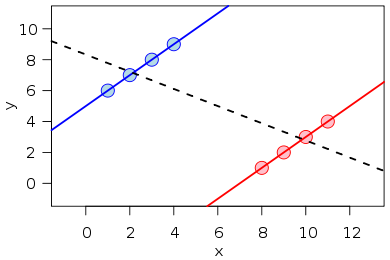
Individually, within the blue and and within the red group we see a positive trend. However, when the data is pooled, that is when we consider the blue and red group together, we see a negative trend. Photo Credit: Wikimedia Commons
The outcomes of lawsuits, promotions, and our choice of medical treatments are frequently based on numerical evidence. Yet our intuition can easily mislead us when we think about numbers. Mathematics and statistics can help — they can give us answers to the question we are asking. But it is up to us to make sure that we are asking the right questions.
I'm Krešimir Josić, at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
The Wikipedia article on Simpson's Paradox has a number of other good examples https://en.wikipedia.org/?title=Simpson's_paradox .
The mathematician John Tukey is credited with saying that "An approximate answer to the right question is worth a great deal more than a precise answer to the wrong question."
This episode was first aired on August 12, 2015