The Power of Cities
by Krešo Josić
Today, let's talk about cities and power laws. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
In the 1930s the Swiss born biologist Max Kleiber studied how much energy different animals expend at rest, and noticed something curious. A human weighs about 10 times more than a cat. But rather than expending 10 times the energy of a resting tabby, we only spend 6 times as much. A cow is about 10 times heavier, and also expends about 6 times the energy of a human at rest.

Max Kleiber (UC Davis)
Kleiber was thus the first to notice that energy expenditure follows a 3/4 power law. What this means is that if you double the size of an animal, it will use about 2^3/4, or about 1.7 times as much energy. If you increase the size tenfold, it will use about 10^3/4 times as much energy. Amazingly organisms from bacteria to whales seem to follow this law.
Power laws are all around us: If you add twice the amount of salt, a dish will not taste twice as salty. Rather, it will appear about 2^1.4 or 2.6 times as salty. A star twice the mass of our Sun will be 10 times as bright. There are many other examples, and surprisingly even human constructs behave similarly. Cities are particularly fascinating: If the size of a city doubles, we see more than a doubling of the number inventors and artists that reside in the city. The number of patents also more than doubles, but, unfortunately, so does the amount of time we spend in traffic. All of these quantities follow power laws.
On the other hand some quantities grow more slowly — if a city doubles in size, we spend less than twice the gasoline or electricity — bigger cities are more efficient. But all is not rosy — the number of crimes and cases of a disease more than double in cities of twice the size.
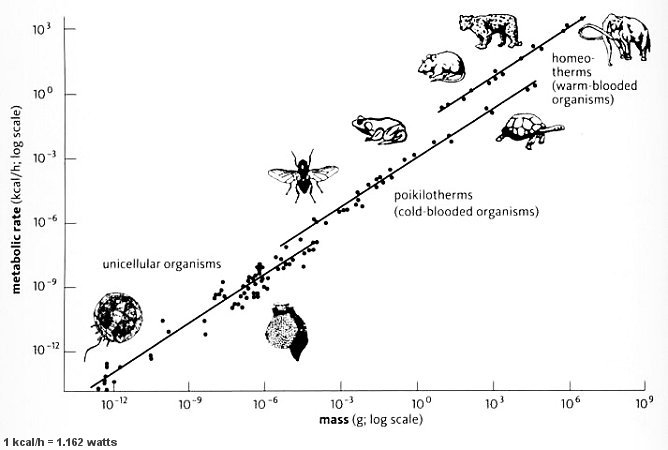
A standard log-log graph of mass vs. metabolic rate. Click on the image to read the review article which provides more information about the data shown in this figure. (Gregory C. O'Kelly/BioMed Central)
We do not yet know exactly why such different quantities as a city's crime rate, road density and the number of inventors behave so predictably. But scientists have plausible theories: It is possible that ideas, information and inspiration behave like diseases, and spread more easily when populations are larger and denser. The larger the city, the more contacts we have, the higher the chance that we will hear the latest important news, or hear about a good job opportunity.
Can we reap the benefits of living in a city — the higher wages, and higher energy efficiency — without the disproportionate increase in crime, pollution and disease? We now know that there are laws that govern how cities grow. This gives me hope that we will also be able to understand the causes of these regularities. Urban planners and administrators will be able to use these insights. Together with physicists and mathematicians they will help cities reach their full potential.
I'm Krešo Josić at the University of Houston, where we are interested in the way inventive minds work.
(Theme music)
Notes and references:
Here is a nice article about Kleiber's Law http://equation-of-the-month.blogspot.com/2012/06/kleiber-law.html. A reason for why it may hold has been proposed in the 1990s. However, it relies on the fractal geometry of the circulatory system, while Kleiber's Law seems to extend to organisms that do not have one. The mechanisms behind the law are therefore still under debate. Indeed, some still argue that this is really a 2/3 power law, and that it has a trivial explanation.
FFor a discussion of power laws and perception you can see this Wikipedia entry on Steven's power law https://en.wikipedia.org/wiki/Stevens%27_power_law. More information about how the luminosity of a star scales with its mass is here http://cseligman.com/text/stars/mldiagram.htm
For a reference on how to explain power law scaling in cities, here is a suggestion by Arbesman, Kleinberg and Strogatz http://arxiv.org/abs/0809.4994. The network of human contacts is assumed to have a hierarchical, self-similar (fractal) structure. Under certain conditions, with an increasing city, the increased number of contacts can lead to the overall benefit of such contacts to grow like a power law. However the assumption that interactions are hierarchical may be too strong. It could be simply the increase in density that facilitates the interchange of ideas and information, as explained here http://arxiv.org/abs/1210.6070 and reviewed here http://newsoffice.mit.edu/2013/why-innovation-thrives-in-cities-0604 Luis Bettencourt's explanation is more complete http://www.sciencemag.org/content/340/6139/1438.
Here are some other interesting short references: A call for a science of cities (polisology?) http://persquaremile.com/2013/06/20/science-of-cities-at-long-last/ and an overview of why innovation thrives in cites http://newsoffice.mit.edu/2013/why-innovation-thrives-in-cities-0604.
Luis Bettencourt and Geoffrey West also give a nice review of the statistical findings and how they could be used. Unfortunately, this article is behind a paywall in Nature http://www.nature.com/nature/journal/v467/n7318/full/467912a.html.
Here is another take on city complexity. http://www.citylab.com/politics/2012/06/mathematical-puzzle-complexity-city/2261/and http://www.citylab.com/design/2012/03/how-big-your-city-really/1444/.
This episode first aired on July 16, 2014.