Cliques and Ties
Today, social cohesion, graph theory, and surveillance. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Science writers Brian Hayes and Steve Lohr discuss modern studies of social grouping. New computational methods are telling us a lot. But many of those methods are the fruit of an old idea called graph theory, which traces to Leonard Euler in 1736.
Euler asked if it were possible for citizens of Königsberg to cross all seven bridges over the Pregel River without recrossing any one. The Bridges connected the land on either side with two islands in the river. By reducing the islands and the lands on the sides to four dots, and the bridges to lines between them, Euler proved that no such path could be found.
Mathematics has since looked at many more problems involving graphs of dots and connections. Social groupings are an example -- connectivity among people. How do we form and sustain our cliques and circles? Another example is connectivity by telephone or Internet. And there our antennae come up.
Can we keep any shred of privacy if the government monitors our communications? But we also remember G. K. Chesterton's famous question, "Where would a wise man hide a leaf?" The answer, of course is "In a forest." How can anyone tease useful intelligence out of hundreds of millions of phone calls or emails? How can one isolate connections among elements of so large a population?
Analysts use ideas from graph theory, bolstered by common sense suppositions, to speed their computational searches for identifiable subgroups. Example: if I know and communicate frequently with two people, the computer will almost certainly find strong links between those two, as well. But I also have weak links to many people, and we can hardly expect much linkage among them.
Once we start focusing on strong links, we discover cliques varying in size from a handful to dozens. In one study of a database of 170 million phone calls, an analyst was able to find almost two hundred thousand groups of three or four. No surprise there -- mostly family groups, one would suppose.
The numbers fall off rapidly with size. Only 21 groups of fifteen. But then they rise again. We find almost a thousand groups of 29 or thirty. And it's those groups that catch our attention. Are these baby-sitting pools, terrorists, or cells of a socialist party? Once we go down that road, we realize that one can root out a journalist and her anonymous contacts.
Here we run up against the oldest axiom of technology: Once invented, any workable idea stays with us. It won't go away. Popes tried to legislate against using crossbows, then firearms. They failed. Nor will these new analytical tools disappear; and we wouldn't want them to. Those same tools serve us every day -- when we use Google, or in separating sound from noise. Of course we'd better find means for preserving some nuggets of our private selves in the midst of it all. And that task grows harder every day.
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
B. Hayes, Connecting the Dots. American Scientist, Vol. 94, Sept-Oct. 2006, pp.400-404.
S. Lohr, Computing, 2016: What Won't Be Possible? The New York Times, Science Times, Tuesday, October 31, 2006, pg. D3.
For more on graph theory, see Wikipedia, https://en.wikipedia.org/wiki/Graph_theory
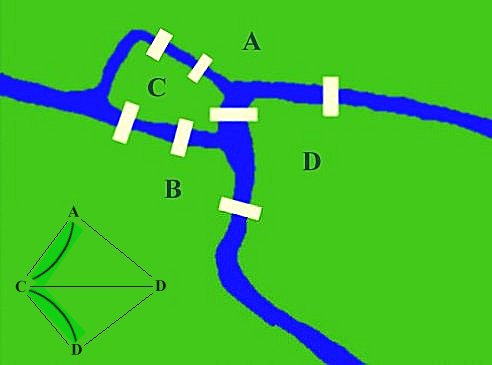
The riddle of the seven bridges of Königsberg