Today, why does sound have a speed? The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

It might seem surprising that sound moves only at one speed in the air around us. Neither pitch nor loudness changes that speed. Isaac Newton tried to explain the speed of sound and got only part of it right. He realized that air is elastic. Try puffing your cheek; then tap on it with your finger. You'd think you were tapping a rubber ball. Compressed air is very springy. 

While we're thinking about bouncing, what happens to a disturbance in open air? The air around us isn't contained like air in our cheeks. Instead of bouncing, a disturbance moves through the air. The combination of the elasticity of a ball combines with its density to set a bouncing frequency. That same combination in open air causes a disturbance, not to bounce, but to travel with a given speed.

Suppose we clap our hands. That creates a sudden high-pressure region that has to move. So the region scoots away in all directions. But it does so with a speed set by the fact that it takes time to compress and release air. And here's the part that Newton got wrong: Since energy rides in the wave, the air warms and cools as its pressure rises and falls. 

The laws of physics dictate the speed of all those processes. Students of engineering or physics learn to calculate the speed of sound using those laws. They show that the speed rises as the square root of absolute temperature. It's around 760 miles an hour at Earth's surface on a warm day, but only 660 at 80,000 feet. 

That's why Mach numbers can be confusing. A Mach number is just a multiple of the speed of sound, which can vary. Mach 2, or twice the speed of sound, is over 1500 miles an hour at Earth's surface, but it's only around 1300 in the cold air at 80,000 feet.

One thing we need to watch here is the idea of frequency. We all know about the frequency of tones -- like an orchestra's A-440. But those frequencies have nothing to do with the air. They're set by the reed in an oboe, or our vocal cords, or a violin string.

On the other hand, a firecracker or, the click of my computer keyboard, is just a spike of pressure without rhythm. The sound of a sinusoidal wave, or a simple bang, both travel the same speed.

By the way, the same physics is at work in other materials. The speed of sound is a lot faster in water -- well over 3000 miles an hour. In steel, it's over 10,000 miles an hour. Both are elastic, but both are a great deal stiffer than air. So, if a friend a mile away hammers a railroad track, the sound takes five seconds to reach us in air. But if we put an ear to the track, we'll hear the hammer blow after only four tenths of a second. 

All this works because air (or steel) is like an elastic spring with each bit of sound doing its long bounce through it. Why do we hear a violinist, a radio, or a friend talking with us? It's because that very physical, very springy, very invisible stuff, called air, both separates us and joins us at the same time.

I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.

This NASA web site offers a nice introductory tutorial on the speed of sound: https://www.grc.nasa.gov/WWW/K-12/airplane/sound.html

The speed of sound,c, is the square root of the partial derivative of pressure with respect to the density of the medium (say air) with the entropy, s, held constant. If one works this out for air, one gets for c, the square root of kRT where R is the ideal gas constant, T is the absolute temperature, and k is the ratio of specific heats at constant pressure and volume. k = 1.405 for air at normal conditions.

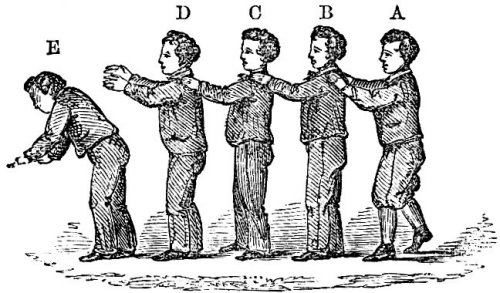
John Tyndall's analogy for the propagation of sound. Boy A pushes boy B who in turn pushes boy C, etc., until boy E falls forward. The boys themselves stay where they are while the disturbance passes through them. The speed of the disturbance is determined by the mass of the boys and the rigidity with which they are in contact. (From J. Tyndall, Sound. (NY: D. Appleton and Co., 1867.)