George Green
Today, a miller takes up mathematics. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
A lifetime of teaching thermal engineering has left my mind littered with names that have no faces. Take the mathematical construction we call a Green's function. First let's meet the function. Then, let's look for the face -- for the person.
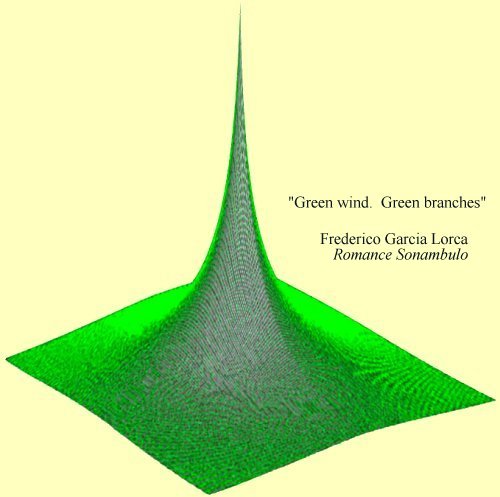
Suppose a large, thin copper plate is at some uniform temperature. Now we imagine a very tiny device that pours out heat: We embed the device at a point in the plate. The resulting plate temperature will spike upward toward infinity at the heat source, and drop off sharply in all directions.
That same spike turns up in many other situations. Push a pointed stick into a rubber membrane and the spike looks just like the temperature spike. George Green was the person who wrote its mathematical form. And, adding many such spikes together, we could now determine effects of complicated heat sources, pressures on membranes, electric fields -- you name it.
George Green was born near Nottingham in 1793, the son of a successful baker. He had to leave primary school, after only two years, to help out in the family business. But, he seems to have been influenced by a fine local math teacher. He was excited by math, and he went on to learn the subject by himself.
When he was fourteen, his father built a fifty-foot grain-grinding windmill in the nearby town of Sneinton. Green moved there to work in it. But he set up a study on the top floor of the mill. He also took up with the mill manager's daughter. For some reason they never married, yet they raised seven children.
The year before his father died, Green published his paper on what came to be known as Green's functions. He was 34, and people like Charles Babbage and John Herschel sat up to take notice.
So Green sold the mill and went to college. First, he filled in gaps in his education at the University of Nottingham. Then he was admitted to Cambridge University. He received a low-grade degree at the age of forty-four -- obviously distracted from his studies by an ongoing production of high-powered mathematical work.
Four years later, now a Fellow at one of the Cambridge Colleges, and pouring forth mathematical works, Green fell ill and returned to Sneinton. He must've known he was dying because he wrote a will leaving everything to his lifelong companion Jane, and their children. He didn't quite make it to the age of forty-eight.
By then he'd written on wave theory, fluid motion, light, electricity. He'd provided a vast understanding of a huge family of problems. His ideas, which are still shaping math, science, and engineering today, did not come out of the limestone halls of Cambridge.
They came instead from a small room in a brick windmill. Colleges are superb places. But Green reminds us they can only support (they can neither create nor replace) the passion for learning and white-hot spikes of understanding, upon which our world turns.
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
P. J. Wallis, Green, George. Dictionary of Scientific Biography (C.C. Gilespie, ed.) New York: Charles Scribner's Sons, 1970-1980.
See also, the entry on George Green in the Dictionary of National Biography.(Leslie Stephen and Sydney Lee, eds.). London: Smith, Elder, and Co., 1908-9.
This website provides a very useful history of Green.
Any reasonably advanced book on calculus or advanced analysis will treat Green's functions, but I especially like H. S. Carslaw and J. C. Jaeger,Conduction of Heat in Solids, Oxford: Oxford University Press, Ch. 14, "The Use of Green's Functions in the Solution of the Equation of Conduction." See also, the excellent website: http://www.engr.unl.edu/~glibrary/home/index.html
My thanks to Lionel E. Davis from the University of Manchester Institute of Science and Technology (UMIST) for suggesting the topic and providing the web material in support of it.