Rocking Boats
Today, we watch boats rocking. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
A listener wrote me with a question about the movement of his WW-II troopship at anchor. I didn't manage to answer his question, but it set me to thinking about something we call a metacenter. I was diverted into thinking about how ships or boats rock back and forth. (So I'm distractable.) Let's think about rocking.
Any floating body has a center of gravity through which its weight acts. This is in the middle of the hull, if the load is balanced. If the boat heels to one side, then the force of gravity will tend to keep it tipping, further and further.
But the boat does not normally capsize because hulls are designed so buoyancy will oppose tipping. Buoyancy acts through the center of gravity, not of the ship, but of the displaced water. We call that point the center of buoyancy. Normally, buoyancy restores the ship to vertical. But there's a catch.
Both gravity and buoyancy act vertically. If a boat lists to one side, then the point where the buoyancy force meets the centerline of the tipped ship, that point had better be above the ship's center of gravity. That point is the metacenter. And, if the metacenter should fall below the ship's center of gravity, it will capsize. And that's were rocking comes in.
A well designed ship bobs back and forth. The larger it is, the slower it rocks. However, we need to watch the metacenter. The center of gravity should be as low as possible and the center of buoyancy should be high. A racing sailboat manages that by having a fairly shallow hull with a deep, heavy keel. It's very hard to tip over; it can heel until its sails almost touch the water.
After a rich haul of crabs, Alaskan crab boats sometimes stack too many heavy crab pots on their decks. That raises the center of gravity without significantly changing the center of buoyancy. The result? The metacenter is now below the center of gravity, and many such boats have abruptly capsized without giving time for the crew to get out or even to send a distress signal.
These same instabilities would be a problem for dirigibles and hot air balloons. However, they normally have very low centers of gravity. Still, just imagine a balloon with the gondola on top. In an airplane, these problems evaporate since buoyancy is negligible in comparison with forces of lift, drag, and thrust.
When we swim, our lungs are high in our bodies, so our center of gravity is relatively low. But a surfer's center of gravity — well that's far above the metacenter. He's unstable, and he constantly has to reposition his center of gravity by leaning right or left.
I suppose these aren't things we incline to think about on our summer vacations. And yet, I find metacentric stability is no less a part of nature's rich texture than the blue sky above, or cool water around us. Now if I can only figure out why that troopship swayed the way it did ...
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
H. W. King, C. O. Wisler, and J. G. Woodburn, Hydraulics. New York: John Wiley & Sons, Inc. 1948. Section 36.
I am grateful to Mechanical Engineering colleague Ralph Metcalfe, and to Edward Morrison for their counsel on this episode. William L. Howard posed the still-unresolved question of the motion of his old troopship. And Edward Morrison adds a fascinating codicil. When the Battleship Texas was modified in 1925-27 its metacentric height (the distance between G and M was increased from 4.5 feet to 10 feet. The unexpected result of the increased stability was difficulty in maneuvering.
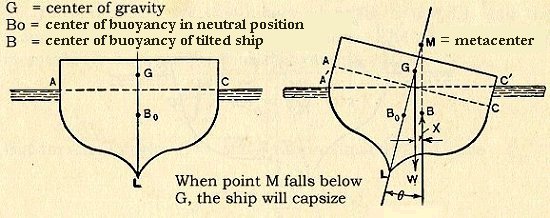
The balance of forces trying to capsize a ship (after King, et al.)