Today, what is 49 from 62? The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.

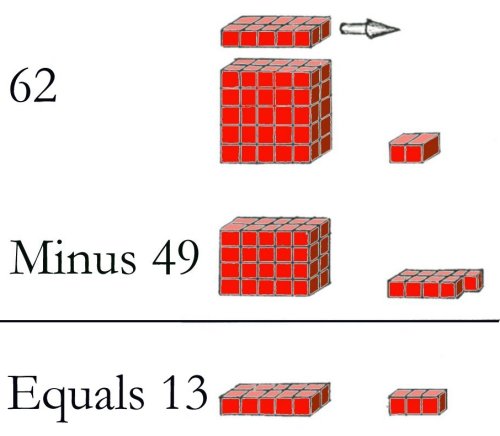
A New York Times piece by Richard Rothstein got my attention. He talks about a battle going on in math education. Look at a simple second-grade problem, he says: "What's 62 minus 49?" Since we have to take nine from the smaller number two in the right-hand column, we borrow a one from the six and turn the two into twelve.

Two schools of thought collide over how we should explain this process to seven-year-olds. Most American teachers will say, "Two and six are neighbors. Just as a good neighbor lends you a cup of sugar, the six lends a one to the two." The borrowing metaphor has a nice sound, but how does it work?

Second-graders need to see that the top number, the 62, can be regarded as either sixty and two or as fifty and twelve. Replace that idea with the metaphor of borrowed sugar, and the notion of moving a block of ten gets lost. Worse yet, we create the impression that the six and the two of 62 are unconnected. We've given the student reliable means for getting an answer. But we've undermined understanding. Short-term gain; long-term loss!

In her fine book, Knowing and Teaching Elementary Mathematics, Dr. Liping Ma uses her Chinese background to help us sift through the problem of subtracting 49 from 62. During China's Cultural Revolution, she was taken from high school and sent off to a poor farming region to be re-educated by peasants. But they turned the tables and asked her to take on the job of teaching their children. From that start, she went on to become a professor at Berkeley.

Long before calculators, the Chinese used the abacus for arithmetic. An abacus represents tens, hundreds, and thousands explicitly. Chinese instruction in arithmetic is accordingly more likely to keep the meanings of decimal places clear.

So I asked friends to do the subtraction in their heads. Then I asked how they did it. Almost none used the conventional method. Most of us have created our own means for breaking down calculations. They say things like, "I take fifty from 62 and then add one." Many then go on to tell stories of trouble with the teachers and other students in second grade. Calling up their first exposure to arithmetic unlocks demons. We do create trouble when we let students get answers using means they don't understand.

I have here an 1853 arithmetic book. In a time with far fewer schools, learning had to be pretty independent. The book uses arrays of blocks to explain the formalisms of arithmetic. It shows how to move ten blocks from the pile of sixty and add them to the two on the right. When you do that, mystery is removed and the problem evaporates. Anyone can see what's happening.

So trouble lurks in this matter. I found one thing very suggestive as I put the question to friends: None actually said the number they got when they took forty-nine away from sixty-two. And I went away wondering if, somehow, they felt it would be unlucky to speak that particular number aloud.

I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.

(Theme music)

Ma, L., Knowing and Teaching Elementary Mathematics. Mahway, NJ: Lawrence Erlbaum Associates, Publishers, 1999.

Rothstein, R., A Sane Position Amid Math's Battlefield. New York Times, Wednesday, June 27, 2001, p. A16.

Fish, D. W., Fish's Arithmetic, Number One. New York: American Book Company, 1853.