Learning What Makes Musical Tones
Today, we learn what makes a musical tone. The University of Houston's College of Engineering presents this series about the machines that make our civilization run, and the people whose ingenuity created them.
Change was afoot by 1600. For 2000 years the alchemical philosophers had tried to understand reality through reason. They'd tried to deduce truth. Now a new breed of philosopher was inventing the process of observation that we call the scientific method.
Take the matter of determining what sound is. Ever since Pythagoras plucked strings around 530 BC, we'd known that the length of a taut string determined its pitch. Pythagoras used different ratios of string length to build musical scales. Halve the length of a string and you raise its pitch an octave. Two-thirds the original length raises the pitch by a fifth (from do to sol), and so forth. Pythagoras couldn't tell us what sound was, but he lent a cosmological significance to different pitches.
By 1600, the last alchemists were still talking about Pythagoras's harmony of the spheres. But the new experimental scientists noticed you could vary pitch without changing a string's length. Galileo's father Vincenzio was a famous lutenist and music theorist. In 1590 he wrote what every lute player knew -- that you changed the pitch of a string by increasing its tension or its density as well as its length. Vincenzio's famous son Galileo clearly explained what that meant. The vibrating string drives vibrations in the air. A pitch is created by air vibrating on the eardrum. The rate of vibration is what determines pitch.
It was Descartes's closest friend and supporter, a philosopher named Marin Marsenne, who converted that to a formula. In 1637 Marsenne published a treatise on music and musical instruments, his Harmonie Universelle. The title was a lingering echo of Pythagoras. But in it Marsenne showed that, while a string's frequency varies directly with its length, it also varies as the square root of the tension divided by the string's density.
Marsenne also recognized overtones, but he was never able to tell there they came from. No one yet understood that a string can support shorter waves along with the one that runs its full length and produces the fundamental tone.
Another question outlived Marsenne: How do vibrations travel in air? Newton finally solved that one in his Principia, but he also came up short. He thought the air temperature stayed constant as sound passed through it. Actually the temperature rises and falls slightly, making sound travel faster than Newton predicted. We didn't get that part right until the 19th century.
An understanding of sound had to be in place before we could do systematic acoustical design of halls or instruments -- before we could standardize pitches (more on that in another episode). It's a simple fact that once we left the old alchemy, not only did our understanding of music change: so too did the very character of the music we listen to today.
I'm John Lienhard, at the University of Houston, where we're interested in the way inventive minds work.
(Theme music)
Dostrovsky, S., Bell, J. F., Truesdell, C., Physics of Music. The New Grove Dictionary of Music & Musicians, (Stanley Sadie, ed.) Vol. 14, pp. 664-677.
Lindley, M., Pythagorean Intonation. The New Grove Dictionary of Music & Musicians, (Stanley Sadie, ed.) Vol. 15, pp. 485-487.
See also the relevant Encyclopaedia Britannica articles.
Tyndall, J., Sound: A Course of Eight lectures Delivered at The Royal Institution of Great Britain. New York: D. Appleton and Company, 1867.
The matter of standardizing pitch is the subject of Episode 1305.
Marsenne's formula actually said that the frequency of a vibrating string varied as the inverse square root of its cross-sectional area. That would be correct so long as all strings were made of the same material. It is more correct to say that it varies in proportion to the string's density expressed in grams per meter of length or pounds per foot of length.
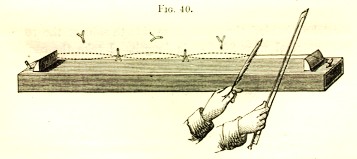
Figure from Tyndall's book on sound showing how one
might bow a Pythagorean monochord to get overtones